三角比の性質

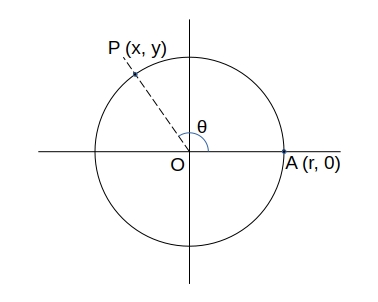
\( \begin{array}{l l}
x = r \cdot \cos \theta & y = r \cdot \sin \theta \\
\end{array}\)

\( \sin^2 \theta + \cos^2 \theta = 1 \)

\( x = r \cdot \cos \theta \)、\( y = r \cdot \sin \theta \) である。
また、\( x^2 + y^2 = r^2 \) であるから、
\(\qquad (r \cdot \cos \theta)^2 + (r \cdot \sin \theta)^2 = r^2 \cdot \cos^2 \theta + r^2 \cdot \sin^2 \theta = r^2 \)
であり、よって、
\(\qquad \sin^2 \theta + \cos^2 \theta = 1 \)

\( \tan^2 \theta + 1 = \dfrac {1}{\cos^2} \)

\( \sin^2 \theta + \cos^2 \theta = 1 \) の両辺を \( \cos^2 \) で割る。

\( \begin{eqnarray}
\dfrac{\sin^2 \theta}{\cos^2 \theta} + \dfrac{\cos^2 \theta}{\cos^2 \theta} &=& \dfrac{1}{\cos^2 \theta} \\[5pt]
\tan^2 \theta + 1 &=& \dfrac{1}{\cos^2 \theta} \\
\end{eqnarray} \)

\( \tan \theta = \displaystyle \frac{ \sin \theta }{ \cos \theta } \)

\( \begin{eqnarray}
\tan \theta &=& \displaystyle \frac{y}{x} \\[5pt]
&=& \displaystyle \frac{\frac{y}{r}}{\frac{x}{r}} \\[5pt]
&=& \displaystyle \frac{ \sin \theta }{ \cos \theta } \\
\end{eqnarray} \)