円のベクトル方程式

3つの定点を \(\ A (\overrightarrow{a})\ \)、\(\ B (\overrightarrow{b})\ \)、\(\ C (\overrightarrow{c})\ \) とし、円周上の任意の点を \(\ P (\overrightarrow{p})\ \) とする。

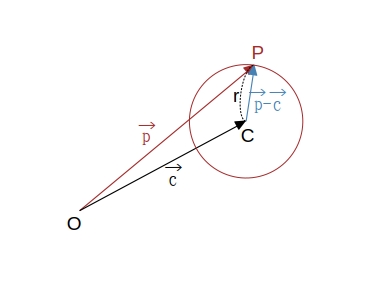
中心 \( C \)、半径 \( r \) の円：\(\ |\ \overrightarrow{p}\ -\ \overrightarrow{c}\ | = r \) または \(\ ( \overrightarrow{p}\ -\ \overrightarrow{c} ) \cdot ( \overrightarrow{p}\ -\ \overrightarrow{c} ) = r^2 \)

\( |\ \overrightarrow{CP}\ | = r \) であるから、\( |\ \overrightarrow{p}\ -\ \overrightarrow{c}\ | = r \)
よって、
\(\qquad |\ \overrightarrow{p}\ -\ \overrightarrow{c}\ |^2 = r^2 \)
ゆえに、
\(\qquad (\overrightarrow{p}\ -\ \overrightarrow{c}) \cdot (\overrightarrow{p}\ -\ \overrightarrow{c}) = r^2 \)

更に、\(\ C (a, b)\ \)、\(\ P (x, y)\ \) として成分で表すと、
\(\qquad \overrightarrow{p}\ -\ \overrightarrow{c}\ =\ (x\ -\ a,\ y\ -\ b) \)
であるから
\(\qquad (x\ -\ a)^2 + (y\ -\ b)^2 = r^2 \)

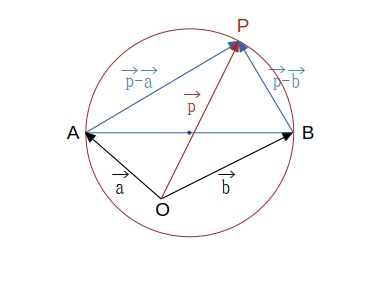
線分 \( AB \) を直径とする円：\( (\overrightarrow{p}\ -\ \overrightarrow{a}) \cdot (\overrightarrow{p}\ -\ \overrightarrow{b}) = 0 \)

半円の弧に対する円周角は直角であるから \(\ AP \perp BP\ \)、または点 \( P \) が \( A \) か \( B \) と一致。
よって
\(\qquad \overrightarrow{AP} \perp \overrightarrow{BP}\ \) または \(\ \overrightarrow{AP} = \overrightarrow{0}\ \) または \(\ \overrightarrow{BP} = \overrightarrow{0} \qquad \) ゆえに \(\qquad \overrightarrow{AP} \cdot \overrightarrow{BP} = 0 \)
よって
\(\qquad (\overrightarrow{OP}\ -\ \overrightarrow{OA}) \cdot (\overrightarrow{OP}\ -\ \overrightarrow{OB}) = 0 \qquad \) したがって \(\qquad (\overrightarrow{p}\ -\ \overrightarrow{a}) \cdot (\overrightarrow{p}\ -\ \overrightarrow{b}) = 0 \qquad \)