ヘロンの公式

\( \triangle ABC \) の面積を \( S \)、\( 2s = a + b + c \) とすると、
\( S = \sqrt{s (s\ -\ a)(s\ -\ b)(s\ -\ c)} \)

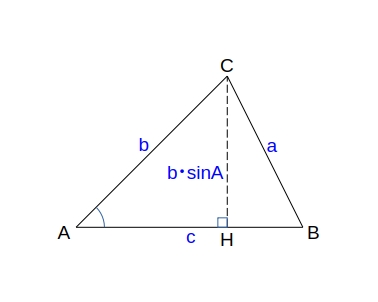
\( \begin{eqnarray*}
S &=& \dfrac {1}{2} bc \cdot \sin A \\
&=& \dfrac {1}{2} bc \sqrt {1\ -\ \cos^2A} \\
&=& \dfrac {1}{2} \sqrt {b^2 c^2 (1\ -\ \cos A)(1 + \cos A)} \\
&=& \dfrac {\sqrt {4 b^2 c^2 (1\ -\ \cos A)(1 + \cos A)}} {4} \cdots ①
\end{eqnarray*} \)

余弦定理から、\( \cos A = \dfrac {b^2 + c^2\ -\ a^2}{2bc} \) であるから、
\( \begin{eqnarray*}
2bc(1 + \cos A) &=& 2bc + 2bc \cdot \cos A \\
&=& 2bc + (b^2 + c^2 -a^2) \\
&=& (b^2 + 2bc + c^2)\ -\ a^2 \\
&=& (b + c)^2\ -\ a^2 \\
&=& (b + c + a)(b + c\ -\ a) \cdots ②\\
2bc(1\ -\ \cos A) &=& 2bc\ -\ 2bc \cdot \cos A \\
&=& 2bc\ -\ (b^2 + c^2 -a^2) \\
&=& a^2\ -\ (b^2\ -\ 2bc + c^2) \\
&=& a^2\ -\ (b\ -\ c)^2\ \\
&=& (a\ -\ b + c)(a + b\ -\ c) \cdots ③\\
\end{eqnarray*} \)

②、③ を ① に代入すると、
\( \begin{eqnarray*}
S &=& \dfrac {\sqrt {(a + b + c)(b + c\ -\ a)(a\ -\ b + c)(a + b\ -\ c)}}{4} \\
&=& \dfrac {\sqrt {(a + b + c)(a + b + c\ -\ 2a)(a + b + c\ -\ 2b)(a + b + c\ -\ 2c)}}{4} \cdots ④
\end{eqnarray*} \)

\( a + b + c = 2s \) として ④ に代入すると、
\( \begin{eqnarray*}
S &=& \dfrac {\sqrt {2s \cdot (2s -\ 2a) \cdot (2s -\ 2b) \cdot (2s -\ 2c)}}{4} \\
&=& \dfrac {\sqrt {2s \cdot 2(s -\ a) \cdot 2(s -\ b) \cdot 2(s -\ c)}}{4} \\
&=& \sqrt {s (s -\ a) (s -\ b) (s -\ c)} \\
\end{eqnarray*} \)