三角形の面積と外接円、内接円

\( \triangle ABC \) の面積を \( S \) とする。

三角形の面積と外接円

\( \triangle ABC \) の外接円の半径を \( R \) とすると、\( S = \dfrac{abc}{4R} \)

正弦定理から \( \sin A = \dfrac {a}{2R} \) であるから、
\( \begin{eqnarray*}
S &=& \dfrac{1}{2} bc \cdot \sin A \\
&=& \dfrac{1}{2} bc \cdot \dfrac {a}{2R} \\
&=& \dfrac{abc}{4R}
\end{eqnarray*} \)

三角形の面積と内接円

\( \triangle ABC \) の内接円の半径を \( r \) とすると、\( S = \dfrac {1}{2}r (a + b + c) \)

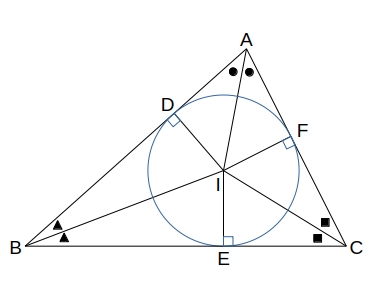
\( \triangle ABC \) の内接円の中心を \( I \) とすると、
\( \begin{eqnarray*}
\triangle ABC &=& \triangle IBC + \triangle ICA + \triangle IAB \\
&=& \dfrac {1}{2} ar + \dfrac {1}{2} br + \dfrac {1}{2} cr \\
&=& \dfrac {1}{2} r(a + b + c)
\end{eqnarray*} \)