三角比の定義
 図形と計算
図形と計算
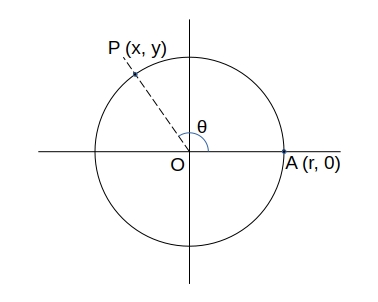
中心が座標軸上の \( 原点 O (0, 0) \) で半径が \( r \) の \( 円O \) で、
円周が \( x軸 \) と交わる点を \( A (r, 0) \)、円周上の任意の点を \( P (x, y) \)、\( \angle AOP \) の角度を \( \theta \) とした時
\( \begin{eqnarray}
\sin x &=& \displaystyle \frac{y}{r} \\
\cos x &=& \displaystyle \frac{x}{r} \\
\tan x &=& \displaystyle \frac{y}{x} \\
\end{eqnarray} \)
とする。
| \( 30^{\circ} \) | \( 45^{\circ} \) | \( 60^{\circ} \) | |
|---|---|---|---|
| \( sin \) | \( \displaystyle \frac{1}{2} \) | \( \displaystyle \frac{1}{ \sqrt{2} } \) | \( \displaystyle \frac{ \sqrt{3} }{2 } \) |
| \( cos \) | \( \displaystyle \frac{ \sqrt{3} }{2} \) | \( \displaystyle \frac{1}{ \sqrt{2} } \) | \( \displaystyle \frac{1}{ {2} } \) |
| \( tan \) | \( \displaystyle \frac{2}{ \sqrt{3} } \) | 1 | \( \sqrt{3} \) |