中線定理

\( \triangle ABC \) において、\( 辺BC \) の中点を \( M \) とすると、
\( AB^2 + AC^2 = 2(AM^2 + BM^2) \)

---

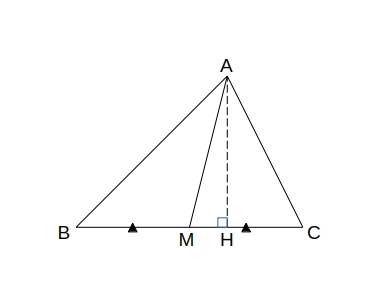
\( 頂点A \) から \( 辺BC \) へ下ろした垂線と \( 辺BC \) の交点を \( H \) とすると、

\( \begin{eqnarray}
AB^2 + AC^2 &=& \{ AH^2 + (BM + MH)^2 \} + \{ AH^2 + (MC – MH)^2 \} \\
&=& \ 2AH^2 + (BM + MH)^2 + (MC – MH)^2 \\
\end{eqnarray} \)

\( BM = MC \) なので、
\( \begin{eqnarray}
\ 2AH^2 + (BM + MH)^2 + (MC – MH)^2 &=& 2AH^2 + (BM + MH)^2 + (BM – MH)^2 \\
&=& 2AH^2 + 2BM^2 + 2MH^2 \\
&=& 2BM^2 + (2AH^2 + 2MH^2) \\
&=& 2BM^2 + 2AM^2 \\
\therefore AB^2 + AC^2 &=& 2(AM^2 + BM^2) \\
\end{eqnarray} \)