正弦定理

\( \triangle ABC \) の外接円の半径が \( R \) の時、
\(
\displaystyle \frac{a}{\sin A} = \displaystyle \frac{b}{\sin B} = \displaystyle \frac{c}{\sin C} = 2R
\)

---

\( \theta = 90^{\circ} \) のとき

\(
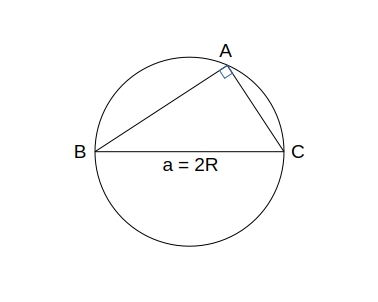
\displaystyle \frac {a}{\sin 90^{\circ}} = \displaystyle \frac {a}{1} = 2R
\)

\( \theta \lt 90^{\circ} \) のとき

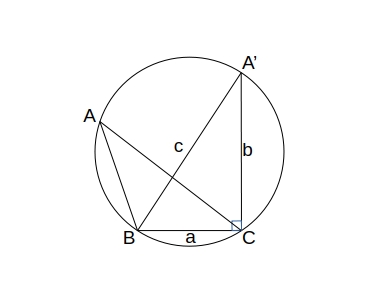
頂点 \( A’ \) は 孤 \( BC \) に対する円周角であり、\( A’B \) は円周の直径なので \( 2R \) である。
\( \begin{eqnarray}
\sin A’ &=& \displaystyle \frac{a}{c} &=& \displaystyle \frac{a}{2R} \\
\displaystyle \frac{a}{\sin A’} &=& 2R
\end{eqnarray} \)
孤 \( BC \) に対する円周角はすべて等しいので \( \angle A = \angle A’ \) であり、
\(
\displaystyle \frac{a}{\sin A} = \displaystyle \frac{a}{\sin A’} = 2R
\)

\( \theta \gt 90^{\circ} \) のとき

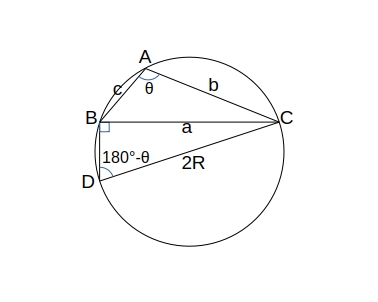
点 \( B \) で \( BC \) と交わる垂線と円周とのもう一方の交点を \( D \) とすると、
円に内接する四角形の対角の和は \( 180^{\circ} \) なので \( \angle D = (180^{\circ} – \angle A) \) である。
また、\( \angle CBD \) は \( 孤CD \) に対する円周角で \( \angle CBD = 90^{\circ} \) なので CD は外接円の直径になる。

\( \begin{eqnarray}
\displaystyle \frac{a}{sin D} &=& \displaystyle \frac{a}{\frac {a}{2R}} \\
&=& 2R \\
\displaystyle \frac{a}{sin D} &=& \displaystyle \frac{a}{sin (180^{\circ} – A)} \\
&=& \displaystyle \frac{a}{sin A} \\
\therefore \displaystyle \frac{a}{sin A} &=& 2R
\end{eqnarray} \)