チェバの定理

\( \triangle ABC \) の \( 頂点 A, B, C \) と１点 \( O \) を結ぶ各直線が対辺またはその延長と交わる点をそれぞれ \( P, Q, R \) とすると、
\( \displaystyle \frac{BP}{PC} \cdot \displaystyle \frac{CQ}{QA} \cdot \displaystyle \frac{AR}{RB} = 1 \)
が成り立つ。
(ただし、\( 点O \) は三角形の辺上にもその延長上にもない。)

---

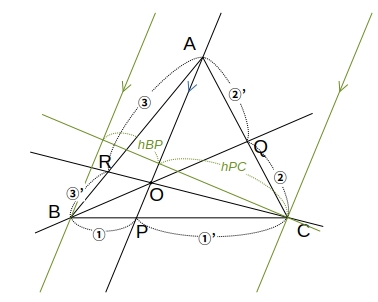
\( \triangle ABO \) と \( \triangle ACO \) は底辺 \( AO \) を共有するので、その面積比はそれぞれの高さの比率に等しく、また、これは \( BP \) と \( PC \) の長さの比とも等しい。
つまり、
\( \displaystyle \frac{BP}{PC} = \displaystyle \frac{\triangle ABO}{\triangle ACO} \qquad \ldots ①\)

同様に、
\( \displaystyle \frac{CQ}{QA} = \displaystyle \frac{\triangle BCO}{\triangle ABO} \qquad \ldots ②\)
\( \displaystyle \frac{AR}{RB} = \displaystyle \frac{\triangle ACO}{\triangle BCO} \qquad \ldots ③\)

\( ①, ②, ③ \) の両辺を乗じると、
\( \begin{eqnarray}
\displaystyle \frac{BP}{PC} \cdot \displaystyle \frac{CQ}{QA} \cdot \displaystyle \frac{AR}{RB} &=& \displaystyle \frac{\triangle ABO}{\triangle ACO} \cdot \displaystyle \frac{\triangle BCO}{\triangle ABO} \cdot \displaystyle \frac{\triangle ACO}{\triangle BCO} \\
&=& 1
\end{eqnarray} \)