メラネウスの定理

\( \triangle ABC \) の \( 辺BC, CA, AB \) またはその延長が頂点を通らない \( 直線l \) とそれぞれ \( P, Q, R \) で交わる時、
\(
\displaystyle \frac{BP}{PC} \cdot \displaystyle \frac{CQ}{QA} \cdot \displaystyle \frac{AR}{RB} = 1
\)
が成り立つ

---

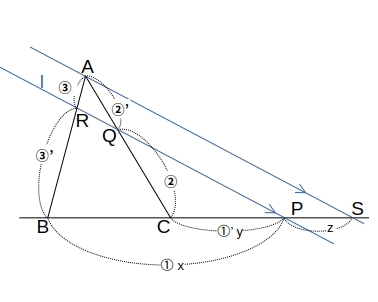
\( A \) を通り \( 直線l \) と平行な直線を引き、BC の延長との交点を \( S \) とする。

\( BP = x, CP = y, PS = z \) とすると、
\( \begin{eqnarray}
\displaystyle \frac{BP}{PC} &=& \displaystyle \frac{x}{y} \qquad \ldots ① \\
\displaystyle \frac{CQ}{QA} &=& \displaystyle \frac{y}{z} \qquad \ldots ② \\
\displaystyle \frac{AR}{RB} &=& \displaystyle \frac{z}{x} \qquad \ldots ③ \\
\end{eqnarray} \)
となる。

これら \( ①, ②, ③ \) の両辺を掛け合わせると、
\( \begin{eqnarray}
\displaystyle \frac{BP}{PC} \cdot \displaystyle \frac{CQ}{QA} \cdot \displaystyle \frac{AR}{RB} &=& \displaystyle \frac{x}{y} \cdot \displaystyle \frac{y}{z} \cdot \displaystyle \frac{z}{x} \\
&=& 1 \\
\end{eqnarray} \)