垂心
 図形の性質
図形の性質三角形の各頂点から対辺またはその延長に下ろした垂線は一点で交わる。
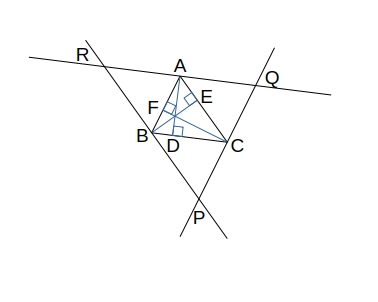
\( \triangle ABC \) で \( 頂点 A \)、\( B \)、\( C \)、から対辺またはその延長に下ろした垂線を \( AD \)、\( BE \)、\( CF \) とする。
また、各頂点を通りそれぞれの対辺と平行な直線を引き、これらの直線が交わる点を上手の通り \( P \)、\( Q \)、\( R \) とする。
\( 四角形 RBCA \)、\( ABCQ \) はともに平行四辺形であるから \( RA = BC = AQ \) である。
また、\( AD \perp BC \) であるから \( AD \perp QR \) でもある。
すなわち、\( AD \) は \( RQ \) の垂直二等分線である。
同様に \( BE \)、 \( CF \) は \( RP \)、 \( PQ \) の垂直二等分線である。
つまり、\( AD \)、 \( BE \)、 \( CF \) は \( \triangle PQR \) の各辺の垂直二等分線であり、これらは一点で交わり交点は \( \triangle PQR \) の外心である。