外心

三角形の3つの辺の垂直二等分線は1点で交わり、その点は3つの頂点から等距離にある。

---

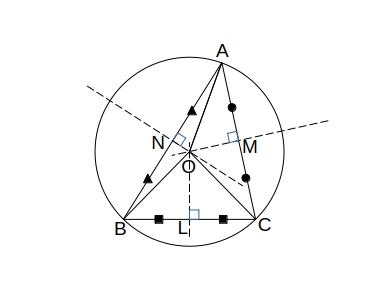
\( \triangle ABC \) において \( 辺AB \) と \( 辺AC \) の垂直二等分線の交点を \( O \)、 \( 辺AB \) と \( 辺AC \) の中点をそれぞれ \( N \)、 \( M \) とする。

\( \triangle AON \) と \( \triangle BON \) は \( 辺ON \) を共有し、\( AN = BN \)、\( \angle ANO = \angle BNO = \angle R \) なので 合同であり、\( AO = BO \) である。
また、\( \triangle AOM \) と \( \triangle BOM \) は同様に合同であり、\( AO = CO \) である。

\( 辺BC \) の中点を \( L \) とすると、\( \triangle BOL \) と \( \triangle COL \) は \( 辺OL \) を共有し、\( BO = CO \)、\( BL = CL \) なので 合同であり、\( \angle BLO = \angle CLO = \angle R\) である。

したがって、
三角形の三辺の垂直二等分線は一点で交わり、その点は３つの頂点から等距離にある。