接弦定理

\( 円O \) の \( 弦AB \) とその \( 接点A \) における \( 接線AT \) が作る \( 角 \angle BAT \) は、その角の内部に含まれる \( 孤AB \) に対する \( 円周角 ACB \) に等しい。

---

\( ① \angle BAT が鋭角の時 \)

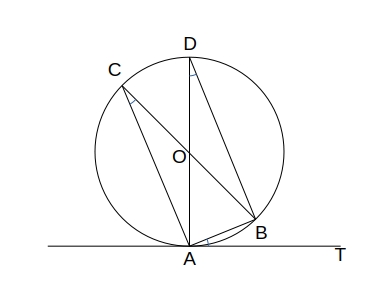
\( A \) を通る直径が円周の反対と交わる点を \( D \) とすると、\( \angle ACB \) と \( \angle ADB \) はともに \( 孤AB \) に対する円周角なので
\( \angle ACB = \angle ADB \)
である。

\( \angle ABD \) は直径に対する円周角なので
\( \angle ABD = \angle R \)
であり、
\( \angle ADB = \angle R – \angle BAD \)
である。

一方で、\( AT \) は \( 円O \) の接線なので \( AT \perp AD \) であり、
\( \angle BAT = \angle R – \angle BAD \)
である。

したがって、
\( \angle BAT = \angle ADB = \angle ACB \)
である。

\( ② \angle BAT が直角の時 \)

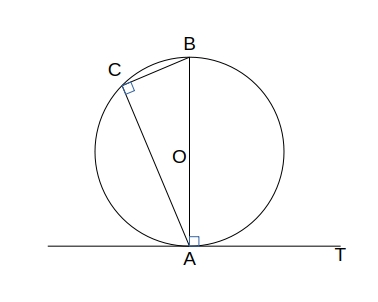
\( AB \perp AT \) なので \( AB \) は \( 円O \) の直径である。
\( \angle ACB \) は直径に対する円周角なので直角であり、
\( \angle BAT = \angle ACB = \angle R \)
である。

\( ③ \angle BAT が鈍角の時 \)

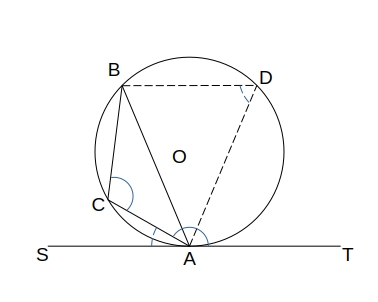
\( AT \) の延長線上、\( A \) に対して \( T \) と反対側に \( 点S \) を取ると、
\( \angle BAT = 180^{\circ} – \angle SAC\)
である。

また、円周上、\( C \) と反対側に \( 点D \) を取ると、\( 四角形 ADBC \) は円に内接する四角形なので対角の和は \( 180^{\circ} \) となり、
\( \angle ACB = 180^{\circ} – \angle ADB \)
である。

① より、
\( \angle SAC = \angle ADB \)
なので、
\( \begin {eqnarray}
\therefore \angle BAT &=& 180^{\circ} – \angle SAC \\
&=& 180^{\circ} – \angle ADB \\
&=& \angle ACB \\
\end{eqnarray} \)