方べきの定理II
図形の性質
円の外部の \( 点P \) から円に引いた接線の接点を T とする。
\( P \) を通る直線がこの円と \( 2点 A, B \) で交わる時、
\( PA \cdot PB = PT^2 \)
が成り立つ。
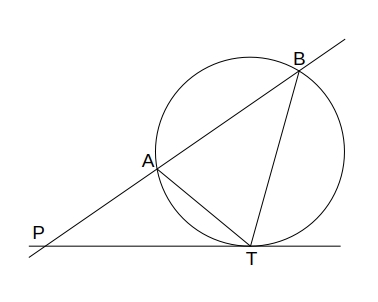
\( \triangle PTA \) と \( \triangle PBT \) において、
接舷定理により \( \angle PTA = \angle PBT \) であり、
\( \angle P \) を共有するので、
\( \triangle PTA \sim \triangle PBT \)
よって、
\( \begin{eqnarray}
PA:PT &=& PT:PB \\
\therefore PA \cdot PB &=& PT^2
\end{eqnarray} \)