数学I・A

数学I
数学A

数学I

数と式

数式の加法、減法、乗法

計算法則

\(A, B, C\) は数式とする。
交換法則 \( \qquad A + B = B + A,\quad AB = BA \)
結合法則 \( \qquad (A + B) + C = A + (B + C),\quad (AB)C = A(BC) \)
分配法則 \( \qquad A(B + C) = AB + AC,\quad (A + B)C = AC + BC \)

指数法則

\( m, n \) は整数とする。

\( a^m a^n = a^{m + n} \)
\( (a^m)^n = a^{mn} \)
\( (ab)^m = a^m b^m \)

(参考) \( a^0 = 1 \)

展開の公式、因数分解

\( (a \pm b)^2 = a^2 \pm 2ab + b^2 \)
\( (a + b)(a\ -\ b) = a^2\ -\ b^2 \)
\( (x + a)(x + b) = x^2 + (a + b)x + ab\)
\( (ax + b)(cx + d) = acx^2 + (ad + bc)x + bd\)
\( (a \pm b)(a^2 \mp ab + b^2) = a^3 \pm b^3 \)
\( (a \pm b)^3 = a^3 \pm 3a^2b + 3ab^2 \pm b^3 \)

実数、平方根

実数の構造

実数	有理数	整数	自然数、0
			負の整数
		分数	有限小数
			循環小数	無限小数
	無理数	循環しない無限少数

絶対値の性質

\( a \geqq 0 \) のとき	\( \|a\| = a \)	\( \|a\|^2 = a^2 \)
\( a \lt 0 \) のとき	\( \|a\| = -a \)	\( \|a\|^2 = a^2 \)

平方根の性質

\( a \geqq 0 \) のとき \(\quad (\sqrt a)^2 = a,\ (- \sqrt a)^2 = a,\ \sqrt a \geqq 0 \)
\( a \geqq 0 \) のとき、\( \quad \sqrt{a^2} = a \)
\( a \lt 0 \) のとき、\( \quad \sqrt{a^2} = -a \)
すなわち、\( \sqrt{a^2} = |a|\)

\( a \gt 0, b \gt 0, k \gt 0 \) のとき

\( \sqrt a \sqrt b = \sqrt {ab} \)
\( \dfrac{\sqrt a}{\sqrt b} = \sqrt{\dfrac{a}{b}} \)
\( \sqrt{k^2a} = k \sqrt a \)

２重根号のはずし方

文字はすべて正の数とする。
\( \sqrt{p \pm k \sqrt{q}} \) は、まず \( \sqrt{( a + b) \pm 2 \sqrt{ab}} \) に変形し、
\( \sqrt{(a + b) + 2 \sqrt{ab}} = \sqrt{a} + \sqrt{b} \)
\( a \gt b \) のとき \( \sqrt{(a + b) – 2 \sqrt{ab}} = \sqrt{a} – \sqrt{b} \)

１次不等式

不等式の性質

\( a \lt b \) ならば \(\quad a + c \lt b + c,\quad a\ -\ c \lt b\ -\ c \)
\( a \lt b, c \gt 0\) ならば \(\quad ac \lt bc,\quad \dfrac{a}{c} \lt \dfrac{b}{c} \)
\( a \lt b, c \lt 0\) ならば \(\quad ac \gt bc,\quad \dfrac{a}{c} \gt \dfrac{b}{c} \)

絶対値を含む方程式・不等式

場合分け \(\quad |A| = \begin{eqnarray}
\left\{
\begin{array}{l}
A\quad &&(A \geqq 0) \\
-A\quad &&(A \lt 0)
\end{array}
\right.
\end{eqnarray} \)
簡便法 \(\quad c \gt 0 \) のとき
方程式 \(\ |x| = c \) の解は \(\quad x = \pm c \)
方程式 \(\ |x| \lt c \) の解は \(\quad -c \lt x \lt c \)
方程式 \(\ |x| \gt c \) の解は \(\quad x \lt -c,\ c \lt x \)

集合

\( U \) は全体集合で、\( A, B, C \) は \( U \) の部分集合

集合の基本

部分集合 \( \cdots A \subset B \)：「\( x \in A\ \) ならば \(\ x \in B\ \)」が成り立つ
相当 \( \cdots A = B \)：「\( A \subset B\ \) かつ \(\ B \subset A\ \)」が成り立つ
共通部分 \( \cdots A \cap B = \{ x\ |\ x \in A\ \) かつ \(\ x \in B \} \)
和集合 \( \cdots A \cup B = \{ x\ |\ x \in A\ \) または \(\ x \in B \} \)
補集合 \( \cdots \overline{A} = \{ x\ |\ x \in U\ \) かつ \(\ x \notin A \} \)

ド・モルガンの法則

\( \overline{A \cup B} = \overline{A} \cap \overline{B} \quad \overline{A \cap B} = \overline{A} \cup \overline{B} \)
\( \overline{A \cup B \cup C} = \overline{A} \cap \overline{B} \cap \overline{C} \quad \overline{A \cap B \cap C} = \overline{A} \cup \overline{B} \cup \overline{C} \)

命題と条件

命題と真偽

真の命題 \(\quad\) 証明する
偽の命題 \(\quad\) 反例を一つあげる

必要・十分条件

２つの条件 \( p, q \) について
\( p \Longrightarrow q \) が真であるとき
\( \quad q \) は \( p \) であるための必要条件
\( \quad p \) は \( q \) であるための十分条件

\( p \Longrightarrow q, q \Longrightarrow p \) がともに真であるとき
\( \quad q \) は \( p \) ( \( p \) は \( q \) ) であるための必要十分条件

命題の逆、対偶、裏

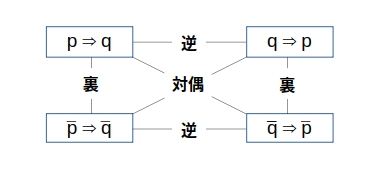
命題とその対偶の真偽は一致する

２次関数

２次関数のグラフ

\( y = a(x\ -\ p)^2 + q \quad (a \neq 0) \) のグラフ

頂点 \( (p, q) \)、軸が \( x = p \) の放物線
\( a \gt 0 \) なら下に凸、\( a \lt 0 \) なら上に凸

\( y = ax^2 + bx + c \quad (a \neq 0) \) のグラフ

右辺を平方完成して、\( y = a(x + \dfrac{b}{2a})^2\ -\ \dfrac{b^2\ -\ 4ac}{4a} \)
頂点 \( (- \dfrac{b}{2a}, – \dfrac{b^2\ -\ 4ac}{4a}) \)、軸が \( x = -\dfrac{b}{2a} \) の放物線
\( a \gt 0 \) なら下に凸、\( a \lt 0 \) なら上に凸

平行移動、対称移動

平行移動

\( x \)軸方向に \( p \)、\( y \)軸方向に \( q \) だけの平行移動で、
点 \( (a, b) \rightarrow (a + p, b + q) \)
グラフ \( y = f(x) \rightarrow y = f(x – p) + q \)

対称移動

	\( x \) 軸	\( y \) 軸	原点
点 \( (a, b) \)	\( (a, -b) \)	\( (-a, b) \)	\( (-a, -b) \)
グラフ \( y = f(x) \)	\( y = -f(x) \)	\( y = f(-x) \)	\( y = -f(-x) \)

関数の最大、最小

２次関数 \( y =ax^2 + bx + c \) の最大・最小

平方完成して \( y = a(x\ -\ p)^2 + q \) の形にする
\( a \gt 0 \) のとき、\( x = p \) で最小値 \( q \)、最大値はない
\( a \lt 0 \) のとき、\( x = p \) で最大値 \( q \)、最小値はない

２次関数 \( y = ax^2 + bx + c\quad (h \leqq x \leqq k) \) の最大・最小

\( a \gt 0 \) (下に凸) の場合

区間の内に頂点があるとき
頂点で最小、頂点から遠い区間の端で最大
区間の外に頂点があるとき
頂点に近い区間の端で最小、遠い端で最大

２次関数の決定

与えられた条件が

放物線の頂点や軸 \( \longrightarrow\quad y= a(x\ -\ p)^2 + q \quad \) とおく
グラフが通る３点 \( \longrightarrow\quad y= ax^2 + bx + c \quad \) とおく

２次方程式の実数解の個数

２次方程式 \(\ y = ax^2 + bx + c\ \) の判別式 \(\ D = b^2\ -\ 4ac\ \) に対し、この２次方程式が

異なる２つの実数解を持つ \(\quad \Longleftrightarrow\quad D \gt 0\)
ただ１つの実数解 (重解) を持つ \(\quad \Longleftrightarrow\quad D = 0\)
実数解をもたない \(\quad \Longleftrightarrow\quad D \lt 0\)

２次関数 \( y = ax^2 + bx + c \) のグラフと \( x \) 軸

２次関数 \( y = ax^2 + bx + c \) のグラフを \( C \)、\( D = b^2 – 4ac \) とすると、

\( D \gt 0\quad \Longleftrightarrow \quad C \) は \( x \) 軸と異なる２点で交わる
\( D = 0\quad \Longleftrightarrow \quad C \) は \( x \) 軸と１点で接する
\( D \lt 0\quad \Longleftrightarrow \quad C \) は \( x \) 軸と共有点を持たない

２次不等式

\( ax^2 + bx + c \gt 0 \)、\( ax^2 + bx + c \lt 0 \) の解

２次方程式 \( ax^2 + bx + c = 0 \) が異なる２つの実数解 \( \alpha, \beta\) をもち、\( \alpha \lt \beta \) とする。\( a \gt 0 \) の場合

\( ax^2 + bx + c \gt 0 \) の解は \( \quad x \lt \alpha,\ \beta \lt x \)
\( ax^2 + bx + c \geqq 0 \) の解は \( \quad x \leqq \alpha,\ \beta \leqq x \)
\( ax^2 + bx + c \lt 0 \) の解は \( \quad \alpha \lt x \lt \beta \)
\( ax^2 + bx + c \leqq 0 \) の解は \( \quad \alpha \leqq x \leqq \beta \)

\( (x\ -\ \alpha)^2 \gt 0 \)、\( (x\ -\ \alpha)^2 \lt 0 \) の解

\( (x\ -\ \alpha)^2 \lt 0 \) の解は \( \quad \) ない
\( (x\ -\ \alpha)^2 \leqq 0 \) の解は \( \quad x = \alpha \)
\( (x\ -\ \alpha)^2 \gt 0 \) の解は \( \quad \alpha \) 以外のすべての実数
\( (x\ -\ \alpha)^2 \geqq 0 \) の解は \( \quad \) すべての実数

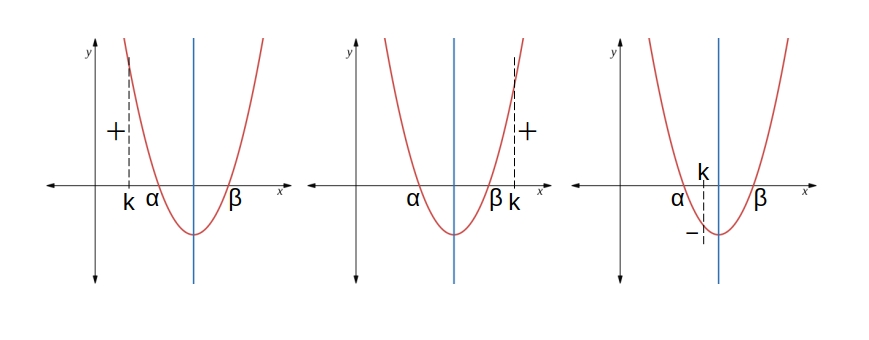
放物線と \( x \) 軸の共有点の位置

\( f(x) = ax^2 + bx + c\quad (a \neq 0),\quad D = b^2\ -\ 4ac \) とする。
放物線 \( y = f(x) \) が \( x \) 軸と \( x = \alpha, \beta\ (\alpha \leqq \beta) \) で共有点を持つとすると、\( a \gt 0 \) のとき

\( \alpha \gt k, \beta \gt k \quad \Longleftrightarrow \quad D \geqq 0,\ 軸 \gt k,\ f(k) \gt 0 \)
\( \alpha \lt k, \beta \lt k \quad \Longleftrightarrow \quad D \geqq 0,\ 軸 \lt k,\ f(k) \gt 0 \)
\( \alpha \lt k \lt \beta \quad \Longleftrightarrow \quad f(k) \lt 0 \)

図形と計量

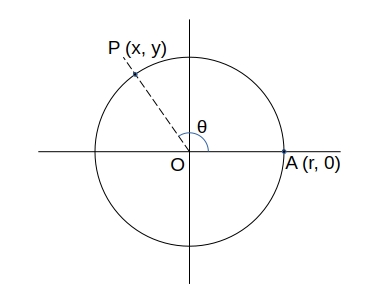
三角比の定義、相関関係

三角比の定義

\( \sin \theta = \dfrac{y}{r} \)
\( \cos \theta = \dfrac{x}{r} \)
\( \tan \theta = \dfrac{y}{x} \)

三角比の相互関係

\( \sin^2 \theta + \cos^2 \theta = 1 \)
\( \tan \theta = \dfrac{\sin \theta}{\cos \theta} \)
\( 1 + \tan^2 \theta = \dfrac{1}{\cos^2 \theta} \)

\( 180^\circ -\ \theta,\ 90^\circ \pm \theta \) の三角比

\( \sin(180^\circ – \theta) = \sin \theta \)
\( \cos(180^\circ – \theta) = – \cos \theta \)
\( \tan(180^\circ – \theta) = – \tan \theta \)
\( \sin(90^\circ \pm \theta) = \cos \theta \)
\( \cos(90^\circ \pm \theta) = \mp \sin \theta \)
\( \tan(90^\circ \pm \theta) = \mp \dfrac{1}{\tan \theta} \qquad \) (複号同順)

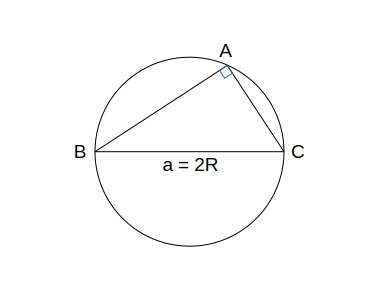
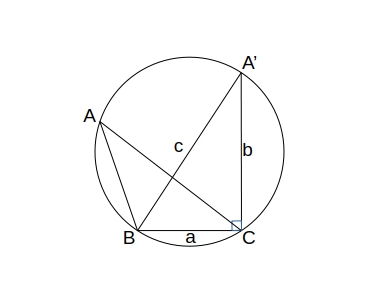
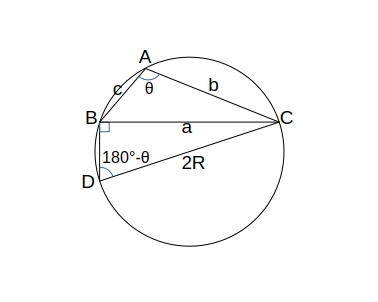
正弦定理

\( \triangle ABC \) の外接円の半径を \( R \) とすると、
\( \dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C} = 2R \)

余弦定理

\( a^2 = b^2 + c^2 -2bc \cos A \qquad a = c \cos B + b \cos C\)
\( b^2 = c^2 + a^2 -2ca \cos B \qquad b = a \cos C + c \cos A\)
\( c^2 = a^2 + b^2 -2ab \cos C \qquad c = b \cos A + a \cos B\)

三角形の辺と角の関係

三角形の成立条件 \( \qquad |b – c| \lt a \lt b + c \)
辺と角の大小関係

\( a \lt b \Longleftrightarrow \angle A \lt \angle B \qquad A \lt 90^\circ \Longleftrightarrow a^2 \lt b^2 + c^2 \)
\( a = b \Longleftrightarrow \angle A = \angle B \qquad A = 90^\circ \Longleftrightarrow a^2 = b^2 + c^2 \)
\( a \gt b \Longleftrightarrow \angle A \gt \angle B \qquad A \gt 90^\circ \Longleftrightarrow a^2 \gt b^2 + c^2 \)

三角形の面積

２辺とその間の角

\( \triangle ABC \) の面積を \( S \) とすると、
\( S = \dfrac{1}{2} bc \sin A = \dfrac{1}{2} ca \sin B = \dfrac{1}{2} ab \sin C \)

３辺 (ヘロン) の公式

\( \triangle ABC \) の面積を \( S \) とし、\( 2s = a + b + c \) とおくと
\( S = \sqrt{s(s – a)(s – b)(s – c)} \)

三角形の外接円、内接円と面積

\( \triangle ABC \) の面積を \( S \)、外接円の半径を \( R \)、内接円の半径を \( r \) とすると
\( S = \dfrac{abc}{4R} \)
\( S = \dfrac{1}{2} r(a + b + c) \)

データの分析

データの代表値

平均値 \( \bar{x} \)

\( \bar{x} = \dfrac{1}{n} (x_1 + x_2 + \cdots + x_n) \)

中央値 (メジアン)

データを値の大きな順に並べたとき中央の位置に来る値。
データの大きさが偶数のときは中央に並ぶ２つの値の平均値。

最頻値 (モード)

データにおける最も個数の多い値。
度数分布表に整理したときは度数が最も大きい階級の階級値。

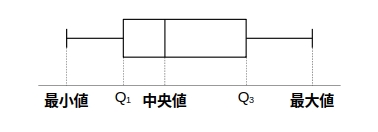
箱ひげ図

データの最小値、第１四分位数 \( Q_1 \)、中央値、第３四分位数 \( Q_3 \)、最大値を箱と線 (ひげ) で表現する図。

分散と標準偏差

偏差

変量 \( x \) の各値と平均値との差 \( \qquad x_1\ -\ \bar{x}, x_2\ -\ \bar{x},\cdots,x_n\ -\ \bar{x} \)

分散

偏差の２乗の平均値 \( \qquad s^2 = \dfrac{1}{n} \{ (x_1\ -\ \bar{x})^2 + (x_2\ -\ \bar{x})^2 + \cdots + (x_n\ -\ \bar{x})^2 \} \)

標準偏差

分散の世の平方根 \(\qquad s = \sqrt{分散} \)

分散と平均値の関係式

\( s^2 = \bar{x^2}\ -\ (\bar{x})^2 \)
\( s = \sqrt{\bar{x^2}\ -\ (\bar{x})^2} \)

共分散

\( s_{xy} = \dfrac{1}{n} \{ (x_1\ -\ \bar{x})(y_1\ -\ \bar{y}) + (x_2\ -\ \bar{x})(y_2\ -\ \bar{y}) + \cdots + (x_n\ -\ \bar{x})(y_n\ -\ \bar{y}) \} \)
\( s_{xy} \gt 0 \) のとき、正の相関関係がある
\( s_{xy} \lt 0 \) のとき、負の相関関係がある

相関係数

変量 \( x, y \) の標準偏差をそれぞれ \( s_x, s_y \) とし、\( x \) と \( y \) の共分散を \( s_{xy} \) とすると、相関係数 \( r \) は
\( r = \dfrac{s_{xy}}{s_x s_y} \quad (-1 \leqq r \leqq 1) \)

２つの変量 \( x, y \) について、それぞれの平均値を \( \bar{x}, \bar{y} \) とし、\( (x\ -\ \bar{x})(y\ -\ \bar{y}) \) の総和を \( a \)、\( (x\ -\ \bar{x})^2 \) の総和を \( b \)、\( (y\ -\ \bar{y})^2 \) の総和を \( c \) とするとき、相関係数 \( r \) は
\( r = \dfrac{a}{\sqrt{b c}} \quad (-1 \leqq r \leqq 1) \)\)

\( r \) が 1 に近いとき、強い正の相関関係がある。
\( r \) が −1 に近いとき、強い負の相関関係がある。
\( r \) が 0 に近いとき、直接的な相関関係はない。

数学A

場合の数と確率

集合の要素の個数

個数定理

\( n(A \cup B) = n(A) + n(B)\ -\ n(A \cap B) \)
\( \qquad A \cap B = \varnothing \) のとき、\( n(A \cup B) = n(A) + n(B) \)
\( n(\bar{A} = n(U)\ -\ n(A) \qquad \) ( \( U \) は全体集合、\( A \) はその部分集合)
\( n(A \cup B \cup C) = n(A) + n(B) + n(C)\ -\ n(A \cap B)\ -\ n(B \cap C)\ -\ n(C \cap A) + n(A \cap B \cap C) \)

集合の要素の個数の性質

\( n(U) \geqq n(A \cup B) \)
\( n(A \cap B) \leqq n(A),\quad n(A \cap B) \leqq n(B) \)
\( n(A \cup B) \leqq n(A) + n(B) \)

場合の数

場合の数の数え方

辞書式配列法や樹形図 (tree) を用いて、もれなく、重複することなく数え上げる。

和の法則、積の法則

和の法則：事柄の \( A, B \) の起こり方がそれぞれ \( a, b \) 通りで、\( A \) と \( B \) が同時に起こらないとき、\( A \) または \( B \) のどちらかが起こる場合の数は \( a + b \) である。
積の法則：事柄 \( A \) の起こり方が \( a \) 通りあり、その各々に対して事柄 \( B \) の起こり方が \( b \) 通りあるとすると、\( A \) と \( B \) がともに起こる場合の数は \( ab \) 通りである。

順列、円順列、重複順列

順列

\( {}_n P_r = n(n\ -\ 1)(n\ -\ 2)\cdots(n\ -\ r + 1) = \dfrac{n!}{(n\ -\ r)!} \qquad (0 \leqq r \leqq n) \)
\( 0! = 1 \)、特に \( {}_n P_n = n!\)

円順列

\( \dfrac{ {}_n P_n }{ n } = (n\ -\ 1)! \)

じゅず順列

\( \dfrac{円順列}{2} = \dfrac{1}{2} \dfrac{ {}_n P_n }{ n } = \dfrac{(n\ -\ 1)!}{2}\)

重複順列

\( n^r \) ( \( n \lt r \) であってもよい )
(例) n個の異なるものを

A, B の２組に分ける \( \qquad \longrightarrow \qquad 2^n\ -\ \underline{ 2 } \quad \) (全てが A または B に入ってしまう２つのパターンを除く)
２組に分ける \( \qquad\qquad \longrightarrow \qquad \dfrac{2^n\ -\ 2}{2} \)
A, B, C の３組に分ける \( \qquad \longrightarrow \qquad 3^n\ -\ \underline{ 3(2^n\ -\ 2)\ -\ 3 } \quad \) (全てが AB, BC, CA のいずれかの２組に入ってしまうパターン、全てが A または B または C に入ってしまうパターンを除く)
３組に分ける \( \qquad\qquad \longrightarrow \qquad \dfrac{ 3^n\ -\ 3(2^n\ -\ 2)\ -\ 3 }{ 3 } \quad \)

組合せ、同じものを含む順列

組合せの数

\( {}_n C_r = \dfrac{ {}_n P_r }{r!} = \dfrac{n!}{(n\ -\ r)!\ r!} \quad(0 \leqq r \leqq n) \qquad \qquad \)特に \( \quad {}_n C_n = 1 \)

\( {}_n C_r \)の性質

\( {}_n C_r = {}_n C_{(n – r)} \quad(0 \leqq r \leqq n) \)
\( {}_n C_r = {}_{n – 1} C_{r – 1} + {}_{n – 1} C_{r} \quad(1 \leqq r \leqq n – 1, n \geqq 2) \)

組分け

n 人を A 組 p 人、B 組 q 人、C 組 r 人に分ける。
\( \quad {}_n C_p \times {}_{n – p} C_q \)
単に３組に分けるときには注意が必要。
\( \quad \) ３組同数なら \( \quad \underline{\div\ 3!} \quad \) (３組の順序を考えない) \( \qquad \qquad \) ２組同数なら \( \quad \underline{\div\ 2!} \quad \) (２組の順序を考えない)

同じものを含む順列

\( {}_{n} C_{p} \times {}_{n-p} C_{q} \times {}_{n-p-q} C_{r} \times \cdots = \dfrac{n!}{p! q! r! \cdots} \qquad \) ただし、\( p + q + r + \cdots = n \)

重複組合せの数

\( {}_n H_r = {}_{n + r -1} C_r \qquad \) ( \( n \lt r\) であってもよい )

確率とその基本性質

確率の定義

全事象 \( U \) のどの根元事象も同様に確からしいとき、事象 \( A \) の起こる確率 \( P(A) \) は
\( P(A) = \dfrac{ n(A) }{ n(U) } = \dfrac{事象 A の起こる場合の数}{起こりうるすべての場合の数} \)

基本性質

\( 0 \leqq P(A) \leqq 1,\quad P(\varnothing) = 0,\quad P(U) = 1 \)

加法定理

事象 \( A, B \) が互いに排反のとき、\( P(A \cup B) = P(A) + P(B) \)

余事象の確率

\( P(\bar{A}) = 1\ -\ P(A) \)

独立な試行、反復試行の確率

独立な試行の確率

２つの独立な試行 \( S, T \) において、\( S \) では事象 \( A \) が起こり、\( T \) では事象 \( B \) が起こるという事象を \( C \) とすると、
\( P(C) = P(A) \cdot P(B) \)

反復試行の確率

１回の試行で事象 \( A \) の起こる確率が \( P \) であるとする。この試行を \( n \) 回繰り返すとき、事象 \( A \) がちょうど \( r \) 回起こる確率は
\( {}_n C_r \cdot P^r \cdot (1\ -\ P)^{n – r} \qquad \) (注意) \( a \neq 0 \) のとき \( a^0 = 1 \)

条件つき確率

事象 \( A \) が起こったときに事象 \( B \) が起こる条件付き確率 \( P_A(B) \) は
\( P_A(B) = \dfrac{n(A \cap B)}{n(A)} = \dfrac{P(A \cap B)}{P(A)} \)

確率の乗法定理

\( P(A \cap B) = P(A) \cdot P(B) \)

図形の性質

三角形の辺の比、外心・内心・重心

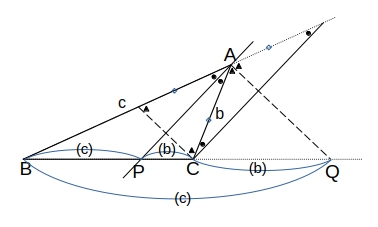
三角形の角の二等分線と比

\( \triangle ABC \) の \( \angle A \) の二等分線と辺 \( BC \) の交点 \( P \) は辺 \( BC \) を \( AB:AC \) に内分する。
\( AB \neq AC \) である \( \triangle ABC \) の \( \angle A \) の外角の二等分線と辺 \( BC \) の延長との交点 \( Q \) は、辺 \( BC \) を \( AB:AC \) に外分する。

外心、内心、重心

外心 O	内心 I	重心 G

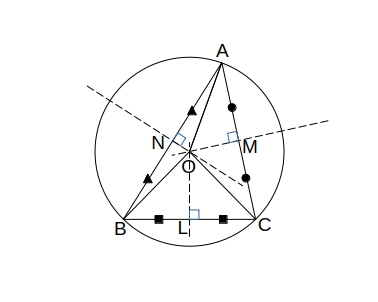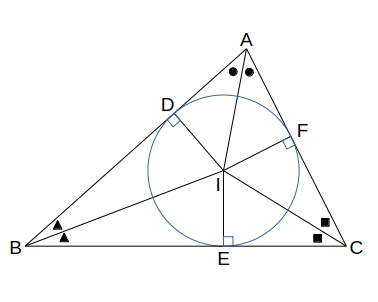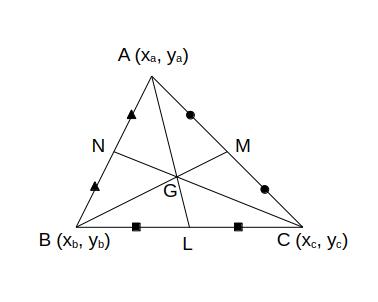垂心

三角形の各頂点から対辺またはその延長に下ろした推薦の交点

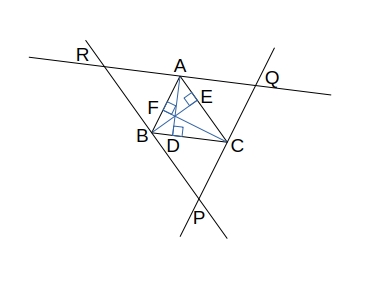
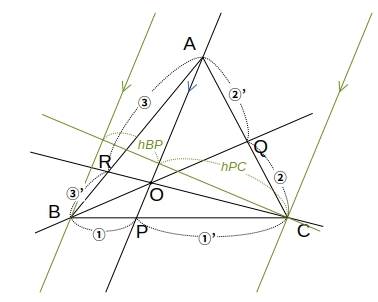
チェバの定理、メラネウスの定理

チェバの定理

\( \triangle ABC \) の頂点 \( A, B, C \) と辺上にもその延長上にもない点 \( O \) を結ぶ各直線が対辺またはその延長とそれぞれ \( P, Q, R \) で交わるとき、
\( \dfrac{BP}{PC} \cdot \dfrac{CQ}{QA} \cdot \dfrac{AR}{RB} = 1 \)

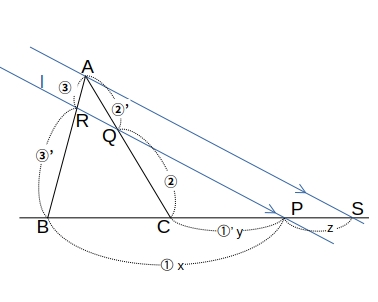
メラネウスの定理

\( \triangle ABC \) の辺 \( BC, CA, AB \) またはその延長が頂点を通らない直線 \( l \) とそれぞれ \( P, Q, R \) で交わるとき、
\( \dfrac{BP}{PC} \cdot \dfrac{CQ}{QA} \cdot \dfrac{AR}{RB} = 1 \)

三角形の３辺の長さの性質

三角形の３辺の長さを \( a, b, c \) とすると、
\( |b\ -\ c| \lt a \lt (b + c) \)

円周角、円に内接する四角形

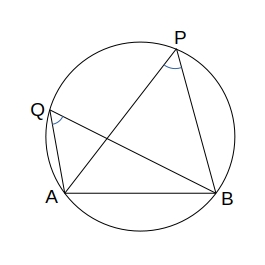
円周角の定理とその逆

４点 \( A, B, P, Q \) で \( P \) と \( Q \) が直線 \( AB \) の同じ側にある時、
\( A, B, P, Q \) が１つの円周上にある \( \quad \Longleftrightarrow \quad \angle APB = \angle AQB \)

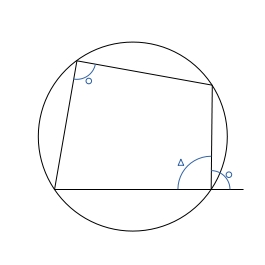
円に内接する四角形

四角形が円に内接するとき、次の ①、② が成り立つ。
① 対角の和は \( 180^\circ \)
② 内角はその対角の外角に等しい
逆に、① または ② が成り立つ四角形は円に内接する。

円と直線、方べきの定理

円の接線

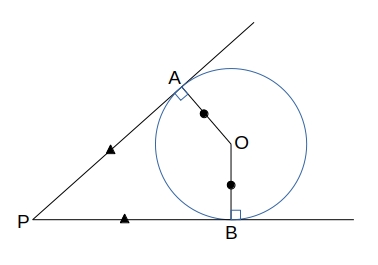
円の接線 \( l \)は接点を通る半径に垂直である
円周上の点 \( A \) を通る直線 \( l \) が半径 \( OA \) と垂直ならば、\( l \) はこの円の接線である。
円の外部の１点からその円に引いた２本の接線の長さは等しい

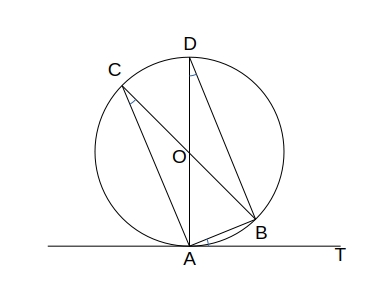
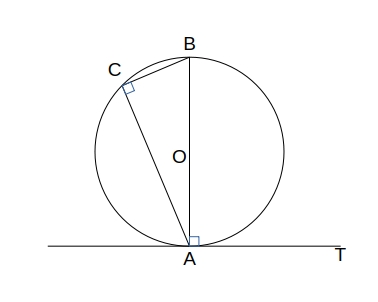
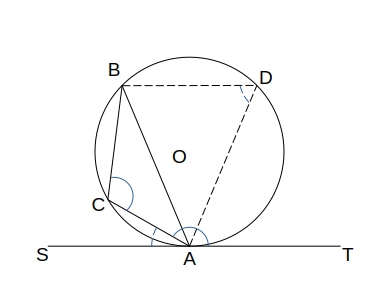
接舷定理とその逆

円 \( O \) の弦 \( AB \) とその端点 \( A \) における接線 \( AT \) で、\( \angle BAT \) はその角の内部に含まれる孤 \( AB \) に対する円周角 \( \angle ACB \) と等しい。
円 \( O \) の孤 \( AB \) と半直線 \( AT \) が直線 \( AB \) の同じ側にあり、孤 \( AB \) に対する円周角 \( \angle ACB \) が \( \angle BAT \) に等しいとき、直線 \( AT \) は点 \( A \) で円 \( O \) に接する。

方べきの定理

円の２つの弦 \( AB, CD \) またはそれらの延長の交点を \( P \) とすると、\( PA \cdot PB = PC \cdot PD \)
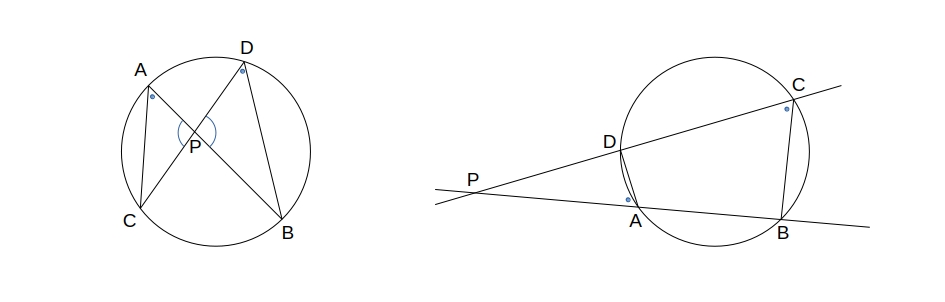
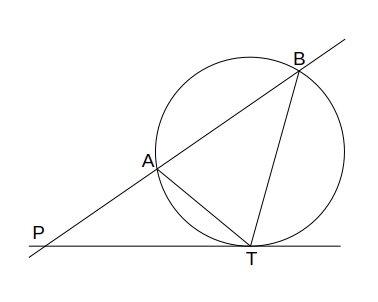
円の外部の点 \( P \) から円に引いた接線の接点を \( T \) とし、\( P \) を通りこの円と２点 \( AB \) で交わる直線を引くと \( PA \cdot PB = PT^2 \)

方べきの定理の逆

２つの線分 \( AB \) と \( CD \)、または \( AB \) の延長と \( CD \) の延長が点 \( P \) で交わるとき、 \( PA \cdot PB = PC \cdot PD \) が成り立つならば４つの点 \( A, B, C, D \) は１つの円周上にある。

三垂線の定理

平面 \( \alpha \) 上に直線 \( l \) があるとき、\( \alpha \) 上にない点 \( A \)、 \( l \) 上の点 \( B \)、\( l \) 上にない \( \alpha \) 上の点 \( O \) について \( AB \perp l \)、\( OB \perp l \)、\( OA \perp OB \) ならば\( OA \perp \alpha \)

\( AB \perp l, OB \perp l \)であるから \( l \perp \) 平面 \( AOB \)
\( l \) に平行で \( O \) を通る直線 \( l’ \) も平面 \( AOB \) と垂直
よって、\( AO \perp l’ \) かつ \( AO \perp OB \) なので \( AO \) は \( \alpha \) に垂直

直線と平面、多面体

空間における直線や平面の位置関係

平行な２直線の一方に垂直な直線は他方にも垂直である。
直線 \( l \) が平面 \( α \) 上の交わる２直線 \( m, n \) に垂直ならば直線 \( l \) は平面 \( \alpha \) に垂直である。
平面 \( \alpha \) の１つの垂線を含む平面は \( \alpha \) に垂直である。

多面体

次の２つの条件を満たす凸多面体を正多面体という。

各平面はすべて合同な正多角形である。
拡張点に集まる麺の数はすべて等しい。

オイラーの多面体定理

凸多面体の頂点の数を \( v \)、辺の数を \( e \) 麺の数を \( f \) とすると
\( v\ -\ e + f = 2 \qquad\qquad\) (「線は帳面に引け」)

整数の性質

約数と倍数

倍数の判定法

２の倍数：一の位が 0, 2, 4, 6, 8 のいずれか
５の倍数：一の位が 0, 5 のいずれか
４の倍数：下２桁が４の倍数
３の倍数：各位の数の和が３の倍数
９の倍数：各位の数の和が９の倍数

約数の個数

自然数 \( N \) の素因数分解が \( N = p^a q^b r^c \cdots \) となるとき、\( N \) の正の約数の個数は
\( (a + 1)(b + 1)(c + 1) \cdots \)

最大公約数、最小公倍数の性質

２つの自然数 \( a, b \) の最大公約数を \( g \)、最小公倍数を \( l \) とする。
\( a = ga’, b = gb’ \) とすると、

\( a’, b’ \) は互いに素である。(\( \pm 1 \) 以外に公約数を持たない)
\( l = ga’b’ = ab’ = a’b\)
\( ab = gl \quad \) 特に \( g = 1 \) のとき、\( ab = l \)

整数の割り算と商、余り

整数の割り算

整数 \( a \) と正の整数 \( b \) に対して、
\( a = bq + r \qquad (0 \geqq r \gt b) \)
を満たす \( q \) と \( r \) がただ１通りに定まる。

連続する整数の積の性質

連続する２つの整数の積は２の倍数である。
連続する３つの整数の積は６の倍数である。

余りによる整数の分類

\( k \) は整数

\( 2k, 2k + 1 \quad \) (偶数、奇数)
\( 3k, 3k + 1, 3k + 2 \quad \) (３で割った余りが 0, 1, 2)
一般に \( m \) が２以上の自然数のとき、\( \quad mk, mk + 1, mk + 2, \cdots , mk + (m\ -\ 1) \)

(参考) 合同式

\( m \) は正の整数
２つ整数 \( a, b \) について \( a\ -\ b \) が \( m \) の倍数であるとき、\( a \) と \( b \) は \( m \) を方として合同であるといい、式で \( a \equiv b \quad (mod\ m) \) と表す。

ユークリッドの互除法・１次不定方程式

割り算と最大公約数

２つの自然数 \( a, b \) について、\( a \) を \( b \) で割ったときの余りを \( r \) とすると、\( a \) と \( b \) の最大公約数は \( b \) と \( r \) の最大公約数に等しい。

ユークリッドの互除法

２つの自然数 \( a, b \) の最大公約数を求めるには次の手順を繰り返せば良い。

\( a \) を \( b \) で割った余りを \( r \) とする
\( r = 0 \quad \Rightarrow \quad b \) が \( a \) と \( b \) の最大公約数
\( r \gt 0 \quad \Rightarrow \quad a \) を \( b \)、\( b \) を \( r \) で置き換えて 1. へ

１次不等式と整数解

\( 0 \) ではない２つの整数 \( a, b \) が互いに素であるならば、任意の整数 \( c \) について \( ax + by = c \) を満たす整数 \( x, y \) が存在する。

分数と小数、\( ｎ \) 進法

有限小数、循環小数の判定

既約分数 \( \dfrac{m}{n} \) について次のことが成り立つ。

分母 \( n \) の素因数は \( 2, 5 \) だけからなる \( \quad \Longleftrightarrow \quad \dfrac{m}{n} \) は有限小数で表される
分母 \( n \) の素因数に \( 2, 5 \) 以外のものがある \( \quad \Longleftrightarrow \quad \dfrac{m}{n} \) は循環小数で表される

\( n \) 進法

位取りの基礎を \( n \) として数を荒らす方法を \( n \) 進法といい、 \( n \) 進法で表された数を \( n \) 進数という。

\( a \geqq 0 \) のとき	\( \|a\| = a \)	\( \|a\|^2 = a^2 \)
\( a \lt 0 \) のとき	\( \|a\| = -a \)	\( \|a\|^2 = a^2 \)