数学II・B

数学II
数学B
1. 数列
2. 統計的な推測

数学II

式と証明

３次式の展開と因数分解

\( \begin{eqnarray}
(a\ +\ b)^3 &=& a^3 + 3a^2b + 3ab^2 + b^3 \\
(a\ -\ b)^3 &=& a^3\ -\ 3a^2b + 3ab^2\ -\ b^3 \\
\end{eqnarray} \)
\( \begin{eqnarray}
(a\ +\ b)(a^2\ -\ ab\ +\ b^2) &=& a^3 + b^3 \\
(a\ -\ b)(a^2\ +\ ab\ +\ b^2) &=& a^3\ -\ b^3 \\
\end{eqnarray} \)

二項定理

\( \begin{eqnarray}
(a + b)^n &=& {}_n C_0\ a^n + {}_n C_1\ a^{n – 1} b^1 + {}_n C_2\ a^{n – 2} b^2 + \cdots + {}_n C_r\ a^{n – r} b^r + \cdots + {}_n C_n-1\ a^1 b^{n – 1} + {}_n C_n\ b^{n} \\
&=& \sum_{r = 0}^n\ {}_n C_r\ a^{n – r} b^r
\end{eqnarray} \)

多項定理

\( p,\ q,\ r \) は整数とする

\( (a + b + c)^n \) の一般項は \( \dfrac{n!}{p! \cdot q! \cdot r!}a^p \cdot b^q \cdot c^r \)
\( \quad p + q + r = n,\quad p \geqq 0,\ q \geqq 0,\ r \geqq 0 \)

整数の割り算

\( A \div B \) の商を \( Q \)、あまりを \( R \) とすると、
\( A = BQ + R \quad (R \) の次数 \(\lt B \) の次数か、 \( R = 0) \)

分数式

\( \dfrac{A}{B} \times \dfrac{C}{D} = \dfrac{AC}{BD},\qquad \dfrac{A}{B} \div \dfrac{C}{D} = \dfrac{A}{B} \times \dfrac{D}{C} = \dfrac{AD}{BC} \)
\( \dfrac{A}{C} + \dfrac{B}{C} = \dfrac{A + B}{C},\qquad \dfrac{A}{C}\ -\ \dfrac{B}{C} = \dfrac{A\ -\ B}{C} \)

恒等式、等式・不等式の証明

恒等式の説明

\( ax^2 + bx + c = a^{\prime}x^2 + b^{\prime}x + c^{\prime} \) が \( x \) の恒等式 \(\quad \Longleftrightarrow \quad a = a^{\prime},\ b = b^{\prime},\ c = c^{\prime} \)

実数の性質

\( a, b \) は整数とする。

\( a^2 \geqq 0,\qquad \qquad a^2 = 0 \quad \Longleftrightarrow \quad a = 0 \)
\( a^2 + b^2 \geqq 0,\qquad a^2 + b^2 = 0 \quad \Longleftrightarrow \quad a = b = 0 \)

コーシー・シュワルツの不等式

\( (a^2 + b^2)(x^2 + y^2) \geqq (ax + by)^2 \)
\( (a^2 + b^2 + c^2)(x^2 + y^2 + z^2) \geqq (ax + by + cz)^2 \)

相加平均 \( \geqq \) 相乗平均

\( a \gt 0,\ b \gt 0 \) のとき、\( \dfrac{a + b}{2} \geqq \sqrt{ab} \qquad \) 等号は \( a = b \) のときに成り立つ

複素数と方程式

複素数

複素数の性質

\( a, b, c, d \) は実数とする。

虚数単位 \( i \qquad i \) は \( i^2 = -1 \) を満たす数
\( a \gt 0 \) のとき、\( \sqrt{-a} = \sqrt{a}i \)
\( a + bi = c + di \quad \Longleftrightarrow \quad a = c \) かつ \( b = d \)

２次方程式の解と判別式

実数係数の２次方程式 \( ax^2 + bx +c = 0 \) の２つの解を \( \alpha, \beta \) とし、判別式を \( D = b^2\ -\ 4ac \) とする。

解の判別

\( D \gt 0 \quad \Longleftrightarrow \quad \) 異なる２つの実数解を持つ
\( D = 0 \quad \Longleftrightarrow \quad \) 重解を持つ
\( D \lt 0 \quad \Longleftrightarrow \quad \) 異なる２つの虚数解を持つ

２次方程式の解と係数の関係

\( \alpha + \beta = – \dfrac{b}{a},\qquad \alpha \beta = \dfrac{c}{a} \)

２次方程式の実数解と実数 \( k \) の大小

\( \alpha, \beta \) が実数のとき、実数 \( k \) に対して
\(
\begin {eqnarray} \left.
\begin {array} {l}
\alpha \gt k \\
\beta \gt k
\end {array}
\right\} \end {eqnarray} \) \(
\quad \Longleftrightarrow \quad D \geqq 0,
\) \(
\begin {eqnarray} \left\{
\begin {array} {l}
(\alpha\ -\ k) + (\beta + k) \gt 0\\
(\beta\ -\ k)(\beta\ -\ k) \gt 0\\
\end {array}
\right. \end {eqnarray}
\)
\(
\begin {eqnarray} \left.
\begin {array} {l}
\alpha \lt k \\
\beta \lt k
\end {array}
\right\} \end {eqnarray} \) \(
\quad \Longleftrightarrow \quad D \geqq 0,
\) \(
\begin {eqnarray} \left\{
\begin {array} {l}
(\alpha\ -\ k) + (\beta + k) \lt 0\\
(\beta\ -\ k)(\beta\ -\ k) \gt 0\\
\end {array}
\right. \end {eqnarray}
\)
\( k \) が \( \alpha \) と \( \beta \) の間 \( \quad \Longleftrightarrow \quad (\alpha\ -\ k)(\beta\ -\ k) \lt 0 \)

剰余の定理と因数定理

剰余定理

\( P(x) \) は整式とする。
\( P(x) \) を１次式 \( x\ -\ a \) で割ったときの余りは \( P(a) \) であり、
\( P(x) \) を１次式 \( ax\ +\ b \) で割ったときの余りは \( P( -\dfrac{b}{a}) \) である。

因数定理

\( P(x) \) は整式とする。
１次式 \( x\ -\ a \) が \( P(x) \) の因数である \( \quad \Longleftrightarrow \quad P(a) = 0 \)
１次式 \( ax\ +\ b \) が \( P(x) \) の因数である \( \quad \Longleftrightarrow \quad P( -\dfrac{b}{a}) = 0 \)

高次方程式

高次方程式の性質

実数係数の \( n \) 次方程式が虚数解 \( a + bi \) ( \(a, b\) は実数) をもつならば、それと共役な複素数 \( a\ -\ bi \) も解である。

３次方程式の解と係数の関係

３次方程式 \( ax^3 + bx^2 + cx + d = 0 \) の３つの解を \( \alpha, \beta, \gamma \) とすると、

\( \alpha + \beta + \gamma = – \dfrac{b}{a},\quad \alpha \beta + \beta \gamma + \gamma \alpha = \dfrac{c}{a},\quad \alpha \cdot \beta \cdot \gamma = – \dfrac{d}{a} \)
\( ax^3 + bx^2 + cx + d = a(x\ -\ \alpha)(x\ -\ \beta)(x\ -\ \gamma) \) が恒等式

図形と方程式

点の座標

点 \( A(x_1, y_1), B(x_2, y_2), C(x_3, y_3) \) とする。

２点間の距離

\( AB = \sqrt{ (x_2\ -\ x_1)^2 + (y_2\ -\ y_1)^2 } \)
特に原点 \( O \) と \( A \) の距離は \( OA = \sqrt{ x_1^2 + y_1^2 } \)

内分点、外分点

線分 \( AB \) を \( m:n \) に分ける点の座標は
内分 \(\cdots \left( \dfrac{nx_1 + mx_2}{m + n}, \dfrac{ny_1 + my_2}{m + n} \right) \)
外分 \(\cdots \left( \dfrac{-nx_1 + mx_2}{m – n}, \dfrac{-ny_1 + my_2}{m – n} \right) \)

重心の座標

\( \triangle ABC \) の重心の座標は
\( \left( \dfrac{x_1 + x_2 + x_3}{3}, \dfrac{y_1 + y_2 + y_3}{3} \right) \)

直線

直線の方程式

\( ax + by + c = 0 \quad (a \neq 0 \) または \( b \neq 0) \)
\( \left[ y = – \dfrac{a}{b}x\ -\ \dfrac{c}{b} \quad ( b \neq 0 ), \qquad x = – \dfrac{c}{a} \quad ( b = 0 ) \right] \)
点 \( (x_1, y_1) \) を通り傾きが \( m \) の直線の方程式は \( y\ -\ y_1 = m(x\ -\ x_1) \)
異なる２点 \( (x_1, y_1), (x_2, y_2) \) を通る直線の方程式は
\( x_1 \neq x_2 \) のとき \( \quad y\ -\ y_1 = \dfrac{ y_2\ -\ y_1}{ x_2\ -\ x_1}(x\ -\ x_1) \)
\( x_1 = x_2 \) のとき \( \quad x = x_1 \)
この２式をまとめると、\( (y_2\ -\ y_1)(x\ -\ x_1)\ -\ (x_2\ -\ x_1)(y\ -\ y_1) = 0 \)

２直線の関係

	\( \begin{eqnarray} \left\{ \begin{array}{l} y = m_1 x + n_1 \\ y = m_2 x + n_2 \end{array} \right. \end{eqnarray} \)	\( \begin{eqnarray} \left\{ \begin{array}{l} a_1 x + b_1 y + c_1 = 0 \\ a_2 x + b_2 y + c_2 = 0 \end{array} \right. \end{eqnarray} \)
交わる	\( m_1 \neq m_2 \)	\( a_1 b_2\ -\ a_2 b_1 \neq 0 \)
平行	\( m_1 = m_2 \)	\( a_1 b_2\ -\ a_2 b_1 = 0 \)
垂直	\( m_1 \cdot m_2 = -1\)	\( a_1 a_2 + b_1 b_2 = 0 \)

一致は平行に含めるものとする

点と直線の距離

直線 \( ax + by + c =0 \) と点 \( (x_1, y_1) \) の距離は
\( \dfrac{ |a x_1 + b y_1 + c | }{ \sqrt{a^2 + b^2} } \)

三角形の面積

３点 \( O (0, 0), A (x_1, y_1), B (x_2, y_2) \) を頂点とする三角形の面積は
\( \dfrac{1}{2} |x_1 y_2 -x_2 y_2 | \)

円

円の方程式

点 \( (a, b) \) を中心とし半径が \( r \) の円の方程式は \( (x\ -\ a)^2 + (y\ -\ b)^2 = r^2 \)
特に原点 \( O \) が中心の場合、\( x^2 + y^2 = r^2 \)
一般形 \( \quad x^2 + y^2 + lx + my + n = 0 \quad \) ただし、\( l^2 + m^2 – 4n > 0 \)

円の接線

円 \( x^2 + y^2 = r^2 \) 上の点 \( (x_1, y_1) \) における円の接線の方程式は
\( x_1 x + y_1 y = r^2 \)

軌跡と方程式

対称移動

点対称：点 \( A \) に対して点 \( P \) と点 \( Q \) が対称 \( \quad \Longleftrightarrow \quad \) 線分 \( PQ \) の中点が \( A \)
線対称：直線 \( l \) に関して点 \( P \) と点 \( Q \) が対称 \( \quad \Longleftrightarrow \quad
\left\{
\begin {array}{l}
1. PQ \perp l \\
2. 線分 PQ の中点が l 上にある
\end {array}
\right. \)

不等式の表す領域

不等式と領域

\( y \gt f(x) \cdots \) 曲線 \( y = f(x) \) の上側の部分
\( y \lt f(x) \cdots \) 曲線 \( y = f(x) \) の下側の部分
\( x^2 + y^2 \lt r^2 \cdots \) 円 \( x^2 + y^2 = r^2 \) の内部
\( x^2 + y^2 \gt r^2 \cdots \) 円 \( x^2 + y^2 = r^2 \) の外部

三角関数

弧度法と三角関数

弧度法

\( 1^\circ = \dfrac{\pi}{180} \) ラジアン、\( \qquad 1 \) ラジアン \( = \left( \dfrac{180}{\pi} \right)^\circ \)
半径 \( r \)、中心角が \( \theta \) ラジアンの扇形の孤の長さは \( r \theta \)、面積は \( \dfrac{1}{2} r^2 \theta \)

三角関数の性質

\( n \) は整数、複号同順

\( \sin (\theta + 2 n \pi) = \sin \theta, \quad \cos (\theta + 2 n \pi) = \cos \theta, \quad \tan (\theta + 2 n \pi) = \tan (\theta + n \pi) = \tan \theta \)
\( \sin (- \theta) = – \sin \theta, \quad \cos (- \theta) = \cos \theta, \quad \tan (- \theta) = – \tan \theta \)
\( \sin (\pi \pm \theta) = \mp \sin \theta, \quad \cos (\pi \pm \theta) = – \cos \theta, \quad \tan (\pi \pm \theta) = \pm \tan \theta \)
\( \sin \left( \dfrac{\pi}{2} \pm \theta \right) = \cos \theta, \quad \cos \left( \dfrac{\pi}{2} \pm \theta \right) = \mp \sin \theta, \quad \tan \left( \dfrac{\pi}{2} \pm \theta \right) = \mp \dfrac {1}{\tan \theta} \)

周期

三角関数の周期

\( k \) は性の定数とする

関数 \( y = \sin k \theta \) の周期 \( \cdots \dfrac {2 \pi}{k} \)
関数 \( y = \cos k \theta \) の周期 \( \cdots \dfrac {2 \pi}{k} \)
関数 \( y = \tan k \theta \) の周期 \( \cdots \dfrac {\pi}{k} \)

加法定理

\( \sin (\alpha \pm \beta) = \sin \alpha \cdot \cos \beta \pm \cos \alpha \cdot \sin \beta \)
\( \cos (\alpha \pm \beta) = \cos \alpha \cdot \cos \beta \mp \sin \alpha \cdot \sin \beta \)
\( \tan (\alpha \pm \beta) = \dfrac{\tan \alpha \pm \tan \beta}{1 \mp \tan \alpha \cdot \tan \beta} \)

２倍角、半角、３倍角の公式

２倍角の公式
- \( \sin 2 \alpha = 2 \cdot \sin \alpha \cdot \cos \alpha \)
- \( \cos 2 \alpha = \cos^2 \alpha\ -\ \sin^2 \alpha = 2 \cos^2 \alpha\ -\ 1 = 1\ -\ 2 \sin^2 \alpha \)
- \( \tan 2 \alpha = \dfrac{2 \tan \alpha}{1\ -\ tan^2 \alpha} \)
半角の公式
- \( \sin^2 \dfrac{\alpha}{2} = \dfrac{1\ -\ \cos \alpha}{2} \)
- \( \cos^2 \dfrac{\alpha}{2} = \dfrac{1 + \cos \alpha}{2} \)
- \( \tan^2 \dfrac{\alpha}{2} = \dfrac{1\ -\ \cos \alpha}{1 + \cos \alpha} \)
３倍角の公式
- \( \sin 3 \alpha = 3 \sin \alpha\ -\ 4 \sin^3 \alpha \)
- \( \cos 3 \alpha = – 3 \cos \alpha + 4 \cos^3 \alpha \)

積 \( \longleftrightarrow \) 和の公式、合成

積 \( \longleftrightarrow \) 和の公式

\( \begin{eqnarray}
\sin \alpha \cdot \cos \beta &=& && \dfrac{1}{2} \{ \sin (\alpha + \beta)\ +\ \sin (\alpha\ -\ \beta) \} \\
\cos \alpha \cdot \sin \beta &=& && \dfrac{1}{2} \{ \sin (\alpha + \beta)\ -\ \sin (\alpha\ -\ \beta) \} \\
\cos \alpha \cdot \cos \beta &=& && \dfrac{1}{2} \{ \cos (\alpha + \beta)\ +\ \cos (\alpha\ -\ \beta) \} \\
\sin \alpha \cdot \sin \beta &=& &-& \dfrac{1}{2} \{ \cos (\alpha + \beta)\ -\ \cos (\alpha\ -\ \beta) \} \\
\end{eqnarray} \)

\( \begin{eqnarray}
\sin A\ +\ \sin B &=& && 2 \sin \dfrac{A + B}{2} \cdot \cos \dfrac{A\ -\ B}{2} \\
\sin A\ -\ \sin B &=& && 2 \cos \dfrac{A + B}{2} \cdot \sin \dfrac{A\ -\ B}{2} \\
\cos A\ +\ \cos B &=& && 2 \cos \dfrac{A + B}{2} \cdot \cos \dfrac{A\ -\ B}{2} \\
\cos A\ -\ \cos B &=& &-& 2 \sin \dfrac{A + B}{2} \cdot \sin \dfrac{A\ -\ B}{2} \\
\end{eqnarray} \)

三角関数の合成

\( (a \neq 0 \) または \( b \neq 0) \)
\( a \sin \theta + b \cos \theta = \sqrt{a^2 + b^2} \sin (\theta + \alpha) \)
ただし、\( \sin \alpha = \dfrac{b}{\sqrt{a^2 + b^2}}, \quad \cos \alpha = \dfrac{a}{\sqrt{a^2 + b^2}} \)

指数関数と対数関数

指数関数の拡張

実数の指数

\( a \gt 0,\ b \gt 0\) で、\( n \) が正の整数、\( r,\ s \) が実数のとき
定義: \( a^0 = 1,\ a^{-n} = \dfrac{1}{a^n} \)
法則: \( a^r a^s = a^{r + s},\ (a^r)^s = a^{rs},\ (ab)^r = a^r b^r \)

累乗根

\( m,\ n,\ p \) は正の整数、\( a \gt 0,\ b \gt 0 \) とする。
\( (\sqrt[n]{a})^n = a,\ \sqrt[n]{a} \sqrt[n]{b} = \sqrt[n]{ab}, \)
\( \dfrac{\sqrt[n]{a}}{\sqrt[n]{b}} = \sqrt[n]{\dfrac{a}{b}},\ (\sqrt[n]{a})^m = \sqrt[n]{a^m}, \)
\( \sqrt[m]{\sqrt[n]{a}} = \sqrt[mn]{a},\ \sqrt[n]{a^m} = \sqrt[np]{a^{mp}}\)

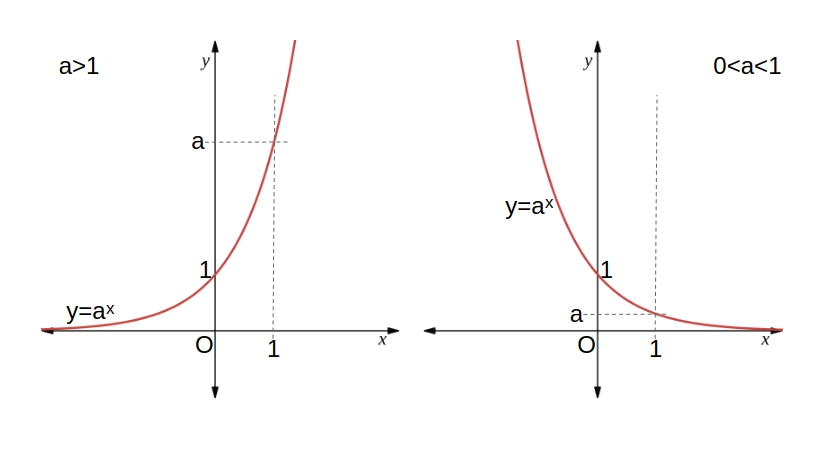
指数関数のグラフ

指数関数 \( y = a^x \ (a \gt 0,\ a \neq 1) \) とそのグラフ

定義域は実数全体、値域は \( y \gt 0 \)
\( a \gt 1 \) のとき \( \quad x \) が増加すると \( y \) も増加
\( 0 \lt a \lt 1 \) のとき \( \quad x \) が増加すると \( y \) は減少
グラフは点 \( (0, 1) \) を通り、\( x \)軸が漸近線

対数とその性質

指数と対数の基本関係

\( a \gt 0,\ a \neq 1,\ M \gt 0 \) とする。
定義 \( \quad a^p = M \iff p = \log_a M\quad[log_a a^p = p]\)
特に \( \log_a a = 1,\ log_a 1 = 0,\ log_a \dfrac{1}{a} = -1 \)

対数の性質

\( a,\ b,\ c \) は \( 1 \) でない正の数、\( M \gt 0,\ N \gt 0,\ k\ \) は実数とする。
\( \log_a MN = \log_a M + \log_a N \),
\( \log_a \dfrac{M}{N} = \log_a M – \log_a N, \quad \log_a M^k = k \log_a M \)
\( \log_a b = \dfrac{\log_c b}{\log_c a}, \quad \log_a b = \dfrac{1}{\log_b a}\)
\( a^{\log_a x} = x \)

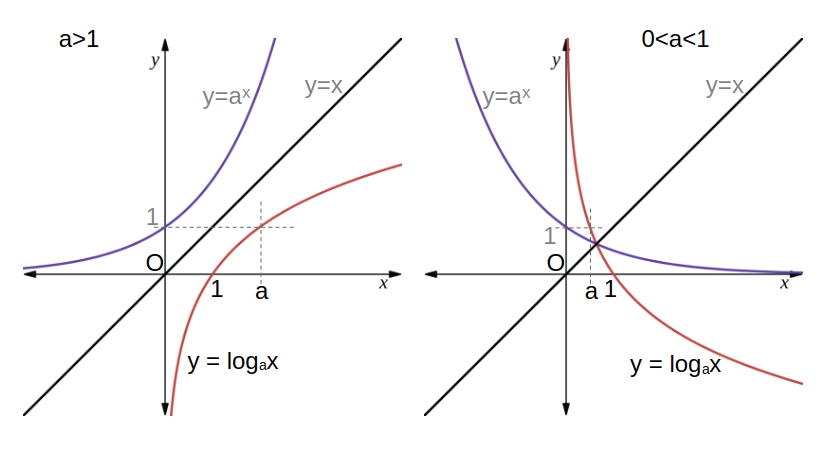
対数関数のグラフ

対数関数 \( y = \log_a x \) とそのグラフ

\( y = \log_a x \) は \( x = a^y \) と同値 \( \quad (a \gt 0, a \neq 1) \)
定義域は \( x \gt 0 \)、値域は実数全体
\( a \gt 1 \) のとき \( \quad x \) が増加すると \( y \) も増加
\( 0 \lt a \lt 1 \) のとき \( \quad x \) が増加すると \( y \) は減少
グラフは点 \( (1, 0) \) を通り、\( y \)軸が漸近線

微分法

微分係数

平均変化率

\( \dfrac{f(b)\ -\ f(a)}{b\ -\ a} \qquad (b \neq a)\)

微分係数

\(\displaystyle f'(a) = \lim_{b\to a} \dfrac{f(b)\ -\ f(a)}{b\ -\ a} = \lim_{h\to 0} \dfrac{f(a + h)\ -\ f(a)}{h} \)

導関数

導関数の定義

定義：\(\displaystyle f'(x) = \lim_{h\to 0} \dfrac{f(x + h) – f(x)}{h} \)

導関数の公式

\( a, b, c, k, l \) は定数、\( n \) は正の整数、\( u \) と \( v \) は \( x \) の関数とする。
\( \begin{align}
&(c)’& &=& &0& \\
&(x^n)’& &=& &nx^{n – 1}& \\
&(ku)’& &=& &ku’& \\
&(u + v)’& &=& &u’ + v’& \\
&(ku + lv)’& &=& &ku’ + lv’& \\
\end{align} \)

（参考）数学III の内容
\( \begin{align}
&(uv)’& &=& &u’v + uv’& \\
&(u^n)’& &=& &nu^{n-1}u’& \\
\end{align} \)
特に \( \{ (ax + b)^n \}’ = na(ax + b)^{n-1} \)

整式の重解条件

整式 \( f(x) \) が \( (x\ -\ \alpha)^2 \) で割り切れるための必要十分条件は
\( \quad f(\alpha) = f'(\alpha) = 0 \)
である。

接線

接線・法線の方程式

法線では \( f'(a) \neq 0 \) とする。
曲線 \( y = f(x) \) 上の点 \( A (a, f(a)) \) における

接線の方程式 \( \qquad y\ -\ f(a) = f'(a)(x\ -\ a) \)
法線の方程式 \( \qquad y\ -\ f(a) = – \dfrac{1}{f'(a)} (x\ -\ a) \)

関数の増減と極大・極小

関数の増減

ある区間で

常に \( f'(x) \gt 0 \) ならば、\( f(x) \) はその区間で単調に増加する。[この区間で接線の傾きは正]
常に \( f'(x) \lt 0 \) ならば、\( f(x) \) はその区間で単調に減少する。[この区間で接線の傾きは負]

関数の極値

極大…増加から減少に移る。\( \qquad f'(x) \) が正 \( \longrightarrow \) 負
極小…減少から増加に移る。\( \qquad f'(x) \) が負 \( \longrightarrow \) 正

最大値・最小値

最大・最小

区間内の極値を求め、その値と区間の両端における関数の値との大小から決定。

積分法

不定積分

導関数と不定積分

\( C \) は積分定数とする。

\( F'(x) = f(x) \) のとき \( \displaystyle \int f(x) dx = F(x) + C \)
\( \displaystyle \int x^n dx = \displaystyle \frac{1}{n + 1} x^{n + 1} + C \qquad \) ( \( n \) は \( 0 \) 以上の整数)
\( \displaystyle \int (ax + b)^n dx = \displaystyle \frac{1}{a} \cdot \frac{1}{n + 1} \cdot (ax + b)^{n + 1} + C \qquad \Longleftarrow \qquad \{ (ax + b)^n \}’ = na(ax + b)^{n-1} \)

不定積分の性質

\( k, l \) は定数とする。

\( \displaystyle \int \{ k f(x) + l g(x) \} dx = k \displaystyle \int f(x) dx + l \displaystyle \int g(x) dx \)

定積分

\( F'(x) = f(x) \) のとき
\( \displaystyle \int_a^b f(x) dx = \Big[ F(x) \Big]_a^b = F(b)\ -\ F(a) \)

定積分の性質

\( k, l \) は定数とする。

\( \displaystyle \int_a^b f(x) dx = \int_a^b f(t) dt \)
\( \displaystyle \int_a^b \{ k f(x) + l g(x) \} dx = k \displaystyle \int_a^b f(x) dx + l \displaystyle \int_a^b g(x) dx \)
\( \displaystyle \int_a^a f(x) dx = 0, \displaystyle \int_b^a f(x) dx = – \displaystyle \int_a^b f(x) dx \)
\( \displaystyle \int_a^b f(x) dx = \displaystyle \int_a^c f(x) dx + \displaystyle \int_c^b f(x) dx \)

偶関数、奇関数の定積分

\( n \) は自然数とする。

\( \displaystyle \int_{-a}^a x^{2n} dx = 2 \displaystyle \int_0^a x^{2n} dx \)
\( \displaystyle \int_{-a}^a x^{2n – 1} dx = 0 \)

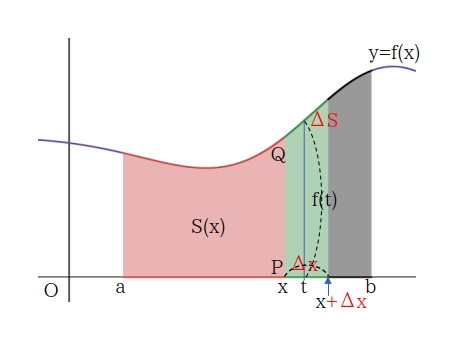
定積分で表された関数

\( x \) は \( t \) に無関係な変数、\( a, b \) は定数とする。

\( \displaystyle \int_a^b f(x, t) dt \) は \( x \) の関数
\( \dfrac{d}{dt} \displaystyle \int_a^x f(t) dt = f(x) \)
\( \displaystyle \int_a^x f(t) dt \) は \( f(x) \) の不定積分

面積

曲線と \( x \) 軸の面積

区間 \( a \leqq x \leqq b \) で常に \( f(x) \geqq 0 \) とする。
曲線 \( y = f(x) \) と \( x \) 軸、および２直線 \( x = a, x = b \) で囲まれた図形の面積 \( S \) は
\( \displaystyle \quad S = \int_a^b f(x) dx \)

区間 \( a \leqq x \leqq b \) で常に \( g(x) \leqq 0 \) とする。
曲線 \( y = g(x) \) と \( x \) 軸、および２直線 \( x = a, x = b \) で囲まれた図形の面積 \( S \) は
\( \displaystyle \quad S =\ – \int_a^b g(x) dx \)
区間 \( a \leqq x \leqq b \) で \( f(x) \geqq 0 \) と \( f(x) \leqq 0 \) の部分がある場合、曲線 \( y = f(x) \) と \( x \) 軸、および２直線 \( x = a, x = b \) で囲まれた図形の面積 \( S \) は
\( \displaystyle \quad S =\ \int_a^b | f(x) | dx \)

２つの曲線の間の面積

区間 \( a \leqq x \leqq b \) で常に \( f(x) \geqq g(x) \) とする。２つの曲線 \( y = f(x), y = g(x) \) および２直線 \( x = a, x = b \) で囲まれた図形の面積 \( S \) は
\( \displaystyle \quad S =\ \int_a^b \{ f(x)\ -\ g(x) \} dx \)

放物線と面積

\( \displaystyle \int_\alpha^\beta (x\ -\ \alpha)(x\ -\ \beta)dx = – \dfrac{1}{6}(\beta\ -\ \alpha)^3 \) を利用。

三次曲線と接線で囲まれた部分の面積

\( \displaystyle \int_\alpha^\beta (x\ -\ \alpha)^2(x\ -\ \beta)dx = – \dfrac{1}{12}(\beta\ -\ \alpha)^4 \)

数学B

数列

等差数列の一般項と和

一般項 \( a_n \)

初項を \( a \)、公差を \( d \) とすると
\( \quad a_n = a + (n\ -\ 1)d \)

等差中項

数列 \( a, b, c \) が等差数列 \( \quad \Longleftrightarrow \quad 2b = a + c \)

等差数列の和

初項から第 \( n \) 項までの和 \( S_n \) は

初項 \( a \)、第 \( n \) 項 (末項) \( l \) に対して、
\( \displaystyle S_n = \dfrac{1}{2} n (a + l) \)
初項 \( a \)、公差 \( d \) に対して、
\( \displaystyle S_n = \dfrac{1}{2} n \{2a + (n\ -\ 1)d \} \)

自然数の和、正の奇数の和

\( \displaystyle 1 + 2 + 3 + \cdots + n = \dfrac{1}{2} n (n + 1) \)
\( 1 + 3 + 5 + \cdots + 2(n\ -\ 1) =n^2 \)
\( \quad \)(初項 \( a = 2 \)、公差 \( d = 2 \) を等差数列の和の公式に代入すると、\( \quad \displaystyle S_n = \dfrac{1}{2} n \{ 2\cdot1 + (n\ -\ 1) \cdot 2 \} = n^2 \quad \) )

等比数列の一般項と和

一般項 \( a_n \)

初項を \( a \)、公比を \( r \) とすると
\( \quad a_n = ar^{n – 1} \)

等比中項

数列 \( a, b, c \) が等比数列 \( \quad \Longleftrightarrow \quad b^2 = ac \)

等比数列の和

初項を \( a \)、公比を \( r \) とする。初項から第 \( n \) 項までの和 \( S_n \) は

\( r \neq 1 \) のとき \( \quad \displaystyle S_n = \dfrac{a(1\ -\ r^n)}{1\ -\ r} = \dfrac{a(r^n\ -\ 1)}{r\ -\ 1} \)
\( r = 1 \) のとき \( S_n = na \)

和の記号 \( \Sigma \)、\( \Sigma \) の性質

和の記号 \( \Sigma \)

\( \quad \displaystyle \sum_{k=1}^n a_k = a_1 + a_2 + a_3 + \cdots + a_n\)

\( \Sigma \) の性質

\( p, q \) は \( k \) に無関係な定数とする。
\( \quad \displaystyle \sum_{k=1}^n (pa_k + qb_k) = p \sum_{k=1}^n a_k + q \sum_{k=1}^n b_k \)

数列の和の公式

\( c, r \) は \( k \) に無関係な定数。

\( \displaystyle \sum_{k=1}^n c = nc \qquad\) 特に \( \quad \displaystyle \sum_{k=1}^n 1 = n \)
\( \displaystyle \sum_{k=1}^n k = \dfrac{1}{2}n(n + 1) \)
\( \displaystyle \sum_{k=1}^n k^2 = \dfrac{1}{6}n(n + 1)(2n + 1) \)
\( \displaystyle \sum_{k=1}^n k^3 = \left\{ \dfrac{1}{2}n(n + 1) \right\}^2 \)
\( \displaystyle \sum_{k=1}^n r^{k-1} = \dfrac{1\ -\ r^n}{1\ -\ r} \qquad (r \neq 1) \)

いろいろな数列

階差数列

数列 \( {a_n} \) の階差数列を \( {b_n} \) とする。
\( \left.
\begin{array} {l}
b_n = a_{n+1}\ -\ a_n \\
n \geqq 2
\end{array}
\quad \right \} \qquad \) のとき \( \qquad \displaystyle a_n = a_1 + \sum_{k=1}^{n-1} b_k\)

和 \( S_n \) と一般項

\( S_n = a_1 + a_2 + \cdots + a_n \quad \) のとき
\( \begin{array} {l}
\quad a_1 = S_1 \\
\quad a_n = S_n\ -\ S_{n-1} \qquad (n \geqq 2)
\end{array} \)

分数の数列の和

部分分数に分解して途中を消す。
\( \displaystyle \dfrac{1}{k(k + 1)} = \dfrac{1}{k}\ -\ \dfrac{1}{k + 1} \)

漸化式の変形、数学的帰納法

漸化式の変形

隣接2項間 \( \quad a_{n+1} = p \cdot a_n + q \quad (p \neq 1) \)
\( \alpha = p \cdot \alpha + q \) を満たす \( \alpha \) に対して
\( a_{n + 1}\ -\ \alpha = p(a_n\ -\ \alpha) \)
隣接3項間 \( \quad p \cdot a_{n+2} + q \cdot a_{n+1} + r \cdot a_n = 0 \)
\( p \cdot x^2 + q \cdot x + r = 0 \) の解を \( \alpha, \beta \) とすると
\( a_{n+2}\ -\ \alpha \cdot a_{n+1} = \beta ( a_{n + 1}\ -\ \alpha \cdot a_n ) \)

数学的帰納法

自然数 \( n \) に関する命題 \( P \) が、すべての自然数 \( n \) について成り立つことを示す手順は

\( n = 1 \) のとき \( P \) が成り立つことを示す。
\( n = k \) のとき \( P \) が成り立つことを仮定して、\( n = k + 1 \) のとき \( P \) が成り立つことを示す。

統計的な推測

確率変数 \( X \) は次の表のような分布に従うとする。

\( X \)	\( x_1 \)	\( x_2 \)	\( \cdots \)	\( x_n \)	計
\( P \)	\( p_1 \)	\( p_2 \)	\( \cdots \)	\( p_3 \)	1

\( p_k\ =\ P(X = x_k) \quad (k\ =\ 1,\ 2,\ \cdots,\ n) \qquad \cdots\ X \) が１つの値 \( x_k \) を取る確率
\( p_1\ \geqq\ 0,\ p_2\ \geqq\ 0,\ \cdots,\ p_n\ \geqq\ 0 \)
\( p_1\ +\ p_2\ +\ \cdots\ +\ p_n\ =\ 1 \)

期待値 \( E(X) \)、分散 \( V(X) \)、標準偏差 \( \sigma (X) \)

\(\displaystyle E(X)\ =\ m\ =\ x_1 p_1\ +\ x_2 p_2\ +\ \cdots\ +\ x_n p_n\ = \sum_{k=1}^n{x_kp_k} \)

\( \displaystyle \begin {eqnarray}
V(X) &=& E((X – m)^2) \\
&=& (x_1\ -\ m)^2 p_1\ +\ (x_2\ -\ m)^2 p_2\ +\ \cdots\ +\ (x_n\ -\ m)^2 p_n \\
&=& \sum_{k=1}^n (x_k\ -\ m)^2 p_k \\
&=& \qquad ({x_1}^2\ -\ 2m x_1\ +\ m^2) p_1\ +\ ({x_2}^2\ -\ 2m x_2\ +\ m^2) p_2\ +\ \cdots\ +\ ({x_n}^2\ -\ 2m x_n\ +\ m^2) p_n \\
&=& \qquad ({x_1}^2 p_1\ +\ {x_2}^2 p_2\ +\ \cdots +\ {x_n}^2 p_n)\ -\ 2m(x_1 p_1\ +\ x_2 p_2\ +\ \cdots\ +\ x_n p_n) \ + m^2 (p_1\ +\ p_2\ +\ \cdots\ +\ p_n)\\
&=& \qquad ({x_1}^2 p_1\ +\ {x_2}^2 p_2\ +\ \cdots +\ {x_n}^2 p_n)\ -\ 2m\cdot m \ + m^2\cdot 1\\
&=& \ E(X^2)\ -\ \{E(X)\}^2
\end {eqnarray} \)

\( \sigma (X)\ =\ \sqrt{V (X)} \)

確率変数の変換

\( X \) は確率変数、\( a, b \) は定数とする。
\( Y = aX + b \) のとき
\( \displaystyle \begin {eqnarray}
E(Y) &=& \qquad \sum_{k=1}^n{y_k p_k} \\
&=& \qquad \sum_{k=1}^n{(a x_k + b) p_k} = a \sum_{k=1}^n{x_k p_k}\ +\ b \sum_{k=1}^n{p_k} \\
&=& a E(X) + b
\end {eqnarray} \)

\( \displaystyle \begin {eqnarray}
V(Y) &=& \qquad \sum_{k=1}^n \{y_k\ -\ E(Y)\}^2 p_k \\
&=& \qquad \sum_{k=1}^n [\ a x_k + b\ -\ \{a E(X) + b\}\ ]^2 p_k = \sum_{k=1}^n [\ a \{x_k\ -\ E(X)\}\ ]^2 p_k = a^2 \sum_{k=1}^n \{x_k\ -\ E(X)\}^2 p_k \\
&=& a^2 V(X)
\end {eqnarray} \)

\( \sigma (Y) = |a| \sigma(X) \)

確率変数の和と積

\( X, Y \) は確率変数、\( a, b \) は定数とする。

\( E( X + Y ) = E(X) + E(Y) \)
\( E( aX + bY ) = a E(X) + b E(Y) \)
\( X \) と \( Y \) が互いに独立ならば
\( E(XY) = E(X) E(Y) \)
\( V( X + Y ) = V(X) + V(Y) \)
\( V( aX + bY ) = a^2V(X) + b^2V(Y) \)

二項分布

二項分布 \( B(n, p) \)

\( P(X = r) = _nC_r p^r q^{n-r} \) で与えられる分布
\( (q = 1\ -\ p;\ r = 0, 1, 2, \cdots, n) \)。
確率変数 \( X \) が二項分布 \( B(n, p) \) に従うとき
平均 \( \quad E(X) = np\)
分散 \( \quad V(X) = npq\)
標準偏差 \( \quad \sigma(X) = \sqrt{npq} \qquad (q = 1 – p)\)

連続型確率変数とその分布

連続型確率変数 \( X \) の確率密度関数 \( f(x) \quad (\alpha \leqq x \leqq \beta) \) について

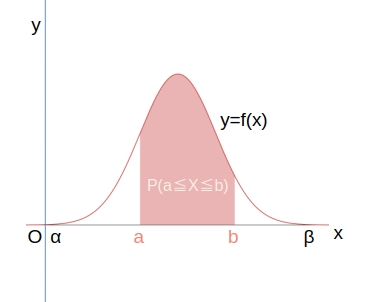
性質：常に
\( f(x) \geqq 0 \),
\( \displaystyle \int_\alpha^\beta{f(x) dx} = 1 \),
\( \displaystyle P(a \leqq X \leqq b) = \int_a^b{f(x) dx} \)
期待値 \( \displaystyle \quad E(X) = m = \int_\alpha^\beta{x f(x) dx}\)
分散 \( \displaystyle \quad V(X) = \int_\alpha^\beta{(x – m)^2 f(x) dx}\)
標準偏差 \( \displaystyle \quad \sigma(X) = \sqrt{V(X)} \)

正規分布

確率変数 \( X \) が正規分布 \( N(m, \sigma^2) \) に従うとき、期待値 \( E(X) =m \), 標準偏差 \( \sigma(X) = \sigma \)

標準化

確率変数 \( X \) が正規分布 \( N(m, \sigma^2) \) に従うとき、\( \displaystyle Z = \dfrac{X – m}{\sigma} \) は標準正規分布 \( N(0, 1) \) に従う。

二項分布の正規分布による近似

二項分布 \( B(n, p) \) に従う確率変数 \( X \) は、\( n \) が大きいとき、近似的に正規分布 \( N(np, np(1 – p)) \) に従う。

母集団と標本

標本平均 \( \overline{X} \)

変量 \( x \) に関する母集団から大きさ \( n \) の無作為標本 \( X_1, X_2, \cdots, X_n,\) を抽出するとき
\( \displaystyle \overline{X} = \dfrac{1}{n}(X_1 + X_2 + \cdots + X_n ) \)

標本平均の期待値・標準偏差

母平均 \( m \), 母標準偏差 \( \sigma \) の母集団から大きさ \( n \) の無作為標本を抽出するとき、標本平均 \( \overline{X} \) の期待値 \( E(\overline{X}) \)、標準偏差 \( \sigma(\overline{X}) \) は
\( \displaystyle E(\overline{X}) = m\)
\( \displaystyle \sigma(\overline{X}) = \dfrac{\sigma}{\sqrt{n}}\)

標本比率

母比率を \( p \)、大きさ \( n \) の無作為標本の標本比率を \( R \) とすると、標本比率の期待値 \( E(R) \)、標準偏差 \( \sigma(R) \) は
\( \displaystyle E(R) = p\)
\( \displaystyle \sigma(R) = \sqrt{ \dfrac{p(1 – p)}{n} }\)

標本平均の分布

母平均 \( m \)、母標準偏差 \( \sigma \) の母集団から大きさ \( n \) の無作為標本を抽出するとき、標本平均 \( \overline X \) は、\( n \) が大きいとき、近似的に正規分布 \( \displaystyle N \left( m, \dfrac{\sigma^2}{n} \right) \) に従う。

仮説検定の手順

事象が起こった状況や原因を推測し、仮説を立てる。
有意水準 \( \alpha \) を定め、仮説に基づいて棄却域を定める。
標本から得られた確率変数の値が棄却域に入れば仮説を棄却し、棄却域に入らなければ仮説を棄却しない。

数学II

式と証明

３次式の展開と因数分解

二項定理

二項定理

多項定理

整数の割り算

分数式

恒等式、等式・不等式の証明

恒等式の説明

実数の性質

コーシー・シュワルツの不等式

相加平均 \( \geqq \) 相乗平均

複素数と方程式

複素数

複素数の性質

２次方程式の解と判別式

解の判別

２次方程式の解と係数の関係

２次方程式の実数解と実数 \( k \) の大小

剰余の定理と因数定理

剰余定理

因数定理

高次方程式

高次方程式の性質

３次方程式の解と係数の関係

図形と方程式

点の座標

２点間の距離

内分点、外分点

重心の座標

直線

直線の方程式

２直線の関係

点と直線の距離

三角形の面積

円

円の方程式

円の接線

軌跡と方程式

対称移動

不等式の表す領域

不等式と領域

三角関数

弧度法と三角関数

弧度法

三角関数の性質

周期

三角関数の周期

加法定理

加法定理

２倍角、半角、３倍角の公式

積 \( \longleftrightarrow \) 和 の公式、合成

積 \( \longleftrightarrow \) 和 の公式

三角関数の合成

指数関数と対数関数

指数関数の拡張

実数の指数

累乗根

指数関数のグラフ

指数関数 \( y = a^x \ (a \gt 0,\ a \neq 1) \) とそのグラフ

対数とその性質

指数と対数の基本関係

対数の性質

対数関数のグラフ

対数関数 \( y = \log_a x \) とそのグラフ

微分法

微分係数

平均変化率

微分係数

導関数

導関数の定義

導関数の公式

整式の重解条件

接線

接線・法線の方程式

関数の増減と極大・極小

関数の増減

関数の極値

最大値・最小値

積 \( \longleftrightarrow \) 和の公式、合成

積 \( \longleftrightarrow \) 和の公式