相加平均と相乗平均
 式と証明
式と証明
\( a \geqq 0, b \geqq 0 \) の時
\[ 相加平均 \displaystyle \frac{a + b}{2} \geqq 相乗平均 \displaystyle \sqrt{ab} \]
であり、等号は \( a = b \) のときに成り立つ。
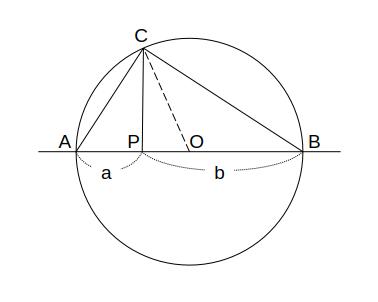
O を中心とする円の直径を AB、円周上の A, B 以外の任意の点を C として、C から AB に対して下ろした垂線と AB の交点を P とする。
また、\( AP = a \)、\( BP = b \) とする。
△APC と △CPB は相似なので、
\( AP:CP = CP:BP \)
よって、
\( \begin{eqnarray}
CP^2 &=& AP \cdot PB = a \cdot b \\
CP &=& \sqrt{ab}
\end{eqnarray} \)
\( 円の半径 CO \geqq CP \) であるから
\( \displaystyle \frac{a + b}{2} \geqq \sqrt{ab} \)
等号が成り立つのは CP が円の半径に等しいとき、つまり、P が O と一致するときで、\( a = b \) のときである。