曲線と \( x \) 軸の間の面積

区間 \( a \leqq x \leqq b \) で常に \( f(x) \geqq 0 \) とする。
\( a \leqq x \leqq b \) であるような任意の実数 \( x \) に対し、点 \( (x, 0), (x, f(x)) \) をそれぞれ \( P, Q \) とする。

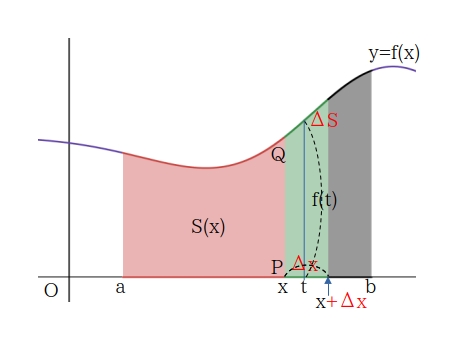
曲線 \( y = f(x) \) と \( x \) 軸、直線 \( x = a \)、直線 \( PQ \) で囲まれた図形の面積を \( S(x) \) とし、\( x, S(x) \) の増分をそれぞれ \( \Delta x (\Delta x \gt 0), \Delta S(x) \) とすると、ある値 \( t (x \leqq t \leqq x + \Delta x)\) に対し、\( \Delta S = f(t) \cdot \Delta x \) とすることができることから、
\( \qquad \displaystyle \dfrac{\Delta S}{\Delta x} = f(t) \)
ここで、\( \Delta x \longrightarrow 0 \) とすると \( t \longrightarrow x \) であるから、
\( \qquad S'(x) = \displaystyle \lim_{\Delta x \to 0} \dfrac{\Delta S}{\Delta x} = f(x) \)
すなわち、\( S(x) \) は \( f(x) \) の１つの不定積分である。したがって、\( f(x) \) の任意の不定積分を \( F(x) \) とすると
\( \qquad S (x) = F(x) + C \qquad \) ( \( C \) は積分定数)
\( S(a) = 0 \quad \) から \( \quad C = -F(a) \quad \) よって、\( \quad S(x) = F(x)\ -\ F(a) \quad \) ゆえに \( S = S(b) = F(b) – F(a) \qquad \) すなわち
\( \qquad S = \displaystyle \Big[ F(x) \Big]_a^b = \int_a^b f(x) dx\)
区間 \( a \leqq x \leqq b \) で常に \( g(x) \leqq 0 \) とする。
\( -g(x) \geqq 0 \) であり、図形の x 軸に関する対称性から、1. により、
\( \qquad S = \displaystyle \int_a^b \{ -g(x) \} dx =\ – \int_a^b \{ g(x) \} dx \)