ベクトルの終点の存在範囲

\(\ \overrightarrow{OA} = \overrightarrow{a}\ \)、\(\ \overrightarrow{OB} = \overrightarrow{b}\ \)、\(\ \overrightarrow{OP} = \overrightarrow{p}\ \) とし、\(\ \overrightarrow{a} \neq \overrightarrow{0}\ \)、\(\ \overrightarrow{b} \neq \overrightarrow{0}\ \)、\(\ \overrightarrow{a}\ /\!/\!\!\!\!\backslash\,\ \overrightarrow{b}\ \)、\(\ \overrightarrow{p} = s \overrightarrow{a} + t \overrightarrow{b}\ \) とする ( \(\ s,\ t\ \) は実数の変数)。点 \( P \) が次のような図形に存在する \(\ s,\ t\ \) の条件は

点 \( P \) が 直線 \( AB \) 上にある \( \qquad \Longleftrightarrow \qquad s + t = 1\)

異なる2点 \(\ A(\overrightarrow{a})\ \)、\(\ B(\overrightarrow{b})\ \) を通る直線のベクトル方程式
特に、\(\ s + t = 1\ \)、\(\ s \geqq 0\ \)、\(\ t \geqq 0\ \) のとき、点 \( P \) は線分 \(\ AB\ \) 上にある。

---

\(\ s = 1\ -\ t \geqq 0\ \) であるから、\(\ t \leqq 1\ \) であり、よって、\(\ 0 \leqq t \leqq 1\ \) である。
このとき、
\(\qquad \overrightarrow{p} = \overrightarrow{a} + t( \overrightarrow{b}\ -\ \overrightarrow{a} ) \)
であるから、点 \(P\) は線分 \(AB\) 上を動く。

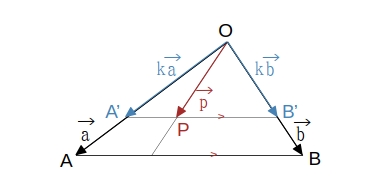
点 \( P \) が \( \triangle OAB \) の周および内部にある \( \qquad \Longleftrightarrow \qquad 0 \leqq s + t \leqq 1,\ s \geqq 0,\ t \geqq 0 \)

\(\ s + t = k\ \)、\( 0 \lt k \leqq 1\ \) とし、\(\ s = s’k\ \)、\(\ t = t’k\ \) とすると、
\(\qquad \overrightarrow{p} = s'(k \overrightarrow{a}) + t'(k \overrightarrow{b} ) \qquad s’ + t’ = 1,\ s’ \geqq 0,\ t’ \geqq 0 \)
ここで、\(\ A'(k \overrightarrow{a})\ \)、\(\ B'(k \overrightarrow{b})\ \) とし、\( k \) を定数 \(\ (k \gt 0)\ \) とすると、点 \( P \) は線分 \( AB \) と 平行 な線分 \( A’B’ \) 上を動く。
そして、\( k \) が \(\ 0 \lt k \leqq 1\ \) で動くと、点 \( A’ \) は線分 \(\ OA\ \) 上を、点 \( B’ \) は線分 \(\ OB\ \) 上を動く。\( k = 0 \) のとき、点 \( P \) は点 \( O \) に一致する。
よって、\(\ 0 \lt k \leqq 1\ \) のとき点 \( P \) は \( \triangle OAB \) の周および内部を動く。

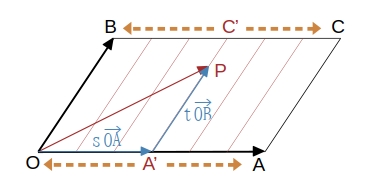
点 \( P \) が 平行四辺形 \( OACB \) の周および内部ある \( \qquad \Longleftrightarrow \qquad 0 \leqq s \leqq 1,\ 0 \leqq t \leqq 1 \)

\( s \) を固定して、\(\ \overrightarrow{OA’} = s \overrightarrow{OA}\ \) とすると \(\ \overrightarrow{OP} = \overrightarrow{OA’} + t \overrightarrow{OB}\ \)
ここで、\( t \) を \(\ 0 \leqq t \leqq 1\ \) の範囲で変化させると、点 \( P \) は下図の線分 \( A’C’ \) 上を動く。そして、\( s \) を \(\ 0 \leqq s \leqq 1\ \) の範囲で変化させると、線分 \( A’C’ \) は 線分 \( OB \) から 線分 \( AC \) まで平行に動く (ただし、\( \overrightarrow{OC} = \overrightarrow{OA} + \overrightarrow{OB} \))。
よって、点 \( P \) は平行四辺形 \( OACB \) の周および内部を動く。