位置ベクトル、ベクトルと図形
 平面上のベクトル
平面上のベクトル位置ベクトル
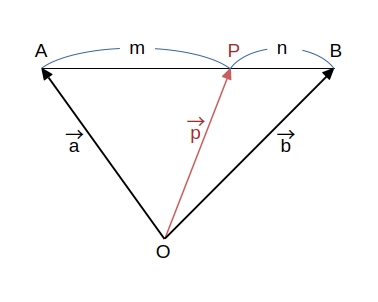
平面上で1点 \( O \) を固定して考えると、任意の点 \( P \) の位置は、ベクトル \( \overrightarrow{p} = \overrightarrow{OP} \) によって定まる。このとき、\( \overrightarrow{p} \) を点 \( O \) に関する点 \( P \) の位置ベクトル といい、\( P( \overrightarrow{p} ) \) と表す。
1点 \( O \) を固定すると、点 \( P \) と 点 \( P \) の位置ベクトル \( \overrightarrow{p} \) を対応させることにより、平面上の各点と平面のベクトルが1対1に対応する。特に、1点 \( O \) を座標平面の原点に取ると、点 \( P \) の座標と \( \overrightarrow{p} \) の成分とは一致する。
また、2点 \( A (\overrightarrow{a}) \)、\( B (\overrightarrow{b}) \) に対し、\( \overrightarrow{AB}\ =\ \overrightarrow{b}\ -\ \overrightarrow{a} \) と表され、\( \overrightarrow{b}\ =\ \overrightarrow{a} \) のとき、点 \( A \) と点 \( B \) は一致する。
線分の内分点の位置ベクトル
2点 \( A ( \overrightarrow{a} ) \)、\( B ( \overrightarrow{b} ) \) を結ぶ線分 \( AB \) を \( m:n \) に内分する点 \( P \)、その位置ベクトルを \( \overrightarrow{p} \) とすると
\(\displaystyle \qquad \overrightarrow{p} = \dfrac{ n \overrightarrow{a} + m \overrightarrow{b} }{ m + n } \)
\(\displaystyle \qquad \overrightarrow{AP} = \dfrac{m}{m + n} \overrightarrow{AB} \)
よって、
\(\displaystyle \qquad \overrightarrow{p}\ -\ \overrightarrow{a} = \dfrac{m}{m + n} ( \overrightarrow{b}\ -\ \overrightarrow{a} ) \)
ゆえに、
\(\displaystyle \qquad \overrightarrow{p}\ = \dfrac{m}{m + n} ( \overrightarrow{b}\ -\ \overrightarrow{a} ) + \overrightarrow{a}\ = \dfrac{ n \overrightarrow{a} + m \overrightarrow{b} }{m + n} \)
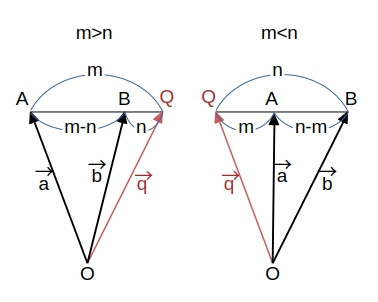
線分の外分点の位置ベクトル
2点 \( A ( \overrightarrow{a} ) \)、\( B ( \overrightarrow{b} ) \) を結ぶ線分 \( AB \) を \( m:n \) に外分する点 \( Q \) の位置ベクトルを \( \overrightarrow{q} \) とすると
\(\displaystyle \qquad \overrightarrow{p} = \dfrac{ – n \overrightarrow{a} + m \overrightarrow{b} }{ m\ -\ n } \)
\( m \gt n \) のとき
\(\displaystyle \qquad \overrightarrow{AQ} = \dfrac{m}{m\ -\ n} \overrightarrow{AB} \)
よって、
\(\displaystyle \qquad \overrightarrow{q}\ = \dfrac{m}{m\ -\ n} ( \overrightarrow{b}\ -\ \overrightarrow{a} ) + \overrightarrow{a}\ = \dfrac{ -n \overrightarrow{a} + m \overrightarrow{b} }{m\ -\ n } \)
\( m \lt n \) のとき
\(\displaystyle \qquad \overrightarrow{AQ} = \dfrac{m}{n\ -\ m} \overrightarrow{BA} \)
よって、
\(\displaystyle \qquad \overrightarrow{q}\ = \overrightarrow{a} + \dfrac{m}{n\ -\ m} ( \overrightarrow{a}\ -\ \overrightarrow{b} ) = \dfrac{ n \overrightarrow{a}\ -\ m \overrightarrow{b} }{n\ -\ m } = \dfrac{ -n \overrightarrow{a} + m \overrightarrow{b} }{m\ -\ n } \)
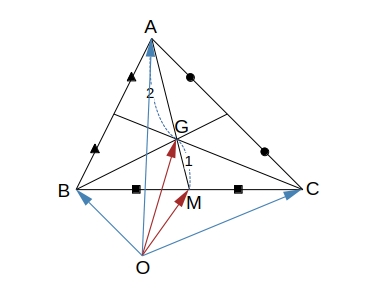
三角形の重心の位置ベクトル
3点 \( A (\overrightarrow{a}) \)、\( B (\overrightarrow{b}) \)、\( C (\overrightarrow{c}) \) を頂点とする \( \triangle ABC \) の重心 \( G \) の位置ベクトルを \( \overrightarrow{g} \) とすると
\(\displaystyle \qquad \overrightarrow{g}\ =\ \dfrac{\overrightarrow{a} + \overrightarrow{b} + \overrightarrow{c}}{3} \)
\( \triangle ABC \) の重心 \( G \) は中線 \( AM \) を \( 2:1 \) に内分するので
\(\displaystyle \qquad \overrightarrow{OG} = \dfrac{\overrightarrow{OA} + 2 \overrightarrow{OM}}{2 + 1} \)
また、
\(\displaystyle \qquad \overrightarrow{OM} = \dfrac{\overrightarrow{OB} + \overrightarrow{OC}}{2} \)
よって、
\(\displaystyle \qquad \overrightarrow{OG} = \dfrac{\overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC}}{3} \)
ゆえに、
\(\displaystyle \qquad \overrightarrow{g}\ =\ \dfrac{\overrightarrow{a} + \overrightarrow{b} + \overrightarrow{c}}{3} \)