直線のベクトル方程式

直線上の任意の点 \( P \) の位置ベクトルを \( \overrightarrow{p} \) とし、\( s \) と \( t \) を実数の変数とする。

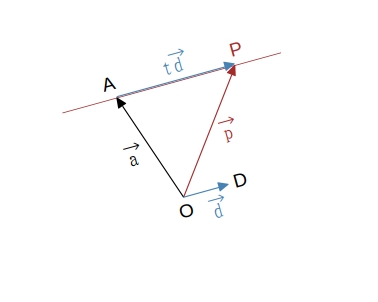
定点 \( A (\overrightarrow{a}) \) を通り、\( \overrightarrow{0} \) でないベクトル \( \overrightarrow{d} \) に平行な直線

\(\qquad \overrightarrow{p} = \overrightarrow{a} + t \overrightarrow{d} \qquad \overrightarrow{d} \) は直線の方向ベクトル

---

下図において
\(\qquad (\overrightarrow{AP} // \overrightarrow{OD} \) または \( \overrightarrow{AP} = \overrightarrow{0}) \)
\(\qquad \Longleftrightarrow \qquad \overrightarrow{AP} = t \overrightarrow{OD} \)
\(\qquad \Longleftrightarrow \qquad \overrightarrow{OP}\ -\ \overrightarrow{OA} = t \overrightarrow{OD} \)
\(\qquad \Longleftrightarrow \qquad \overrightarrow{p}\ -\ \overrightarrow{a} = t \overrightarrow{d} \)
であるから、\(\qquad \overrightarrow{p} = \overrightarrow{a} + t \overrightarrow{d} \cdots \) ①

このとき、\( \overrightarrow{d} \) を直線 ① の 方向ベクトル、\( t \) を 媒介変数 という。
更に、原点を \( O \)、点 \( A(x_1,\ y_1) \)、直線 ① 上の任意の点を \( P (x,\ y) \) とし、\( \overrightarrow{d} = (l,\ m) \) とすると、① から
\(\qquad (x,\ y) = (x_1,\ y_1) + t(l,\ m) = (x_1 + tl,\ y_1 + tm) \)
すなわち、
\(\displaystyle \qquad \begin{eqnarray} \left\{ \begin{array} {l}
x = x_1 + tl\\
y = y_1 + tm
\end{array} \right. \end{eqnarray} \cdots \) ②
連立方程式 ② を直線①の 媒介変数表示 という。

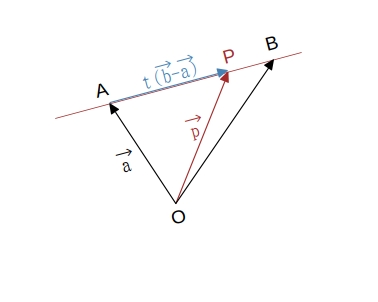
異なる2点 \( A(\overrightarrow{a}) \)、\( B(\overrightarrow{b}) \) を通る直線

\(\qquad \overrightarrow{p} = (1\ -\ t)\overrightarrow{a} + t \overrightarrow{b} \qquad \) または \(\qquad \overrightarrow{p} = s \overrightarrow{a} + t \overrightarrow{b}, \quad s + t = 1 \)

---

\( \overrightarrow{d} = \overrightarrow{AB} \) のとき、\( \overrightarrow{AB} = \overrightarrow{b}\ -\ \overrightarrow{a} \) であるから、直線 \( AB \) のベクトル方程式は
\(\qquad \overrightarrow{p} = \overrightarrow{a} + t (\overrightarrow{b}\ -\ \overrightarrow{a}) \)
すなわち
\(\qquad \overrightarrow{p} = (1\ -\ t) \overrightarrow{a} + t \overrightarrow{b} \)