極方程式

極方程式

ある曲線が極座標 \( (r,\ \theta) \) に関する方程式 \( r\ =\ f(\theta) \) や \( F (r,\ \theta)\ =\ 0 \) で表されるとき、この方程式を曲線の 極方程式 という。
極方程式では \( r\ \lt 0 \) の場合も扱う。すなわち、\( r\ \gt\ 0 \) のときの点 \( (-r, \theta) \) は点 \( (r, \theta\ +\ \pi) \) と同じものと考える。

円

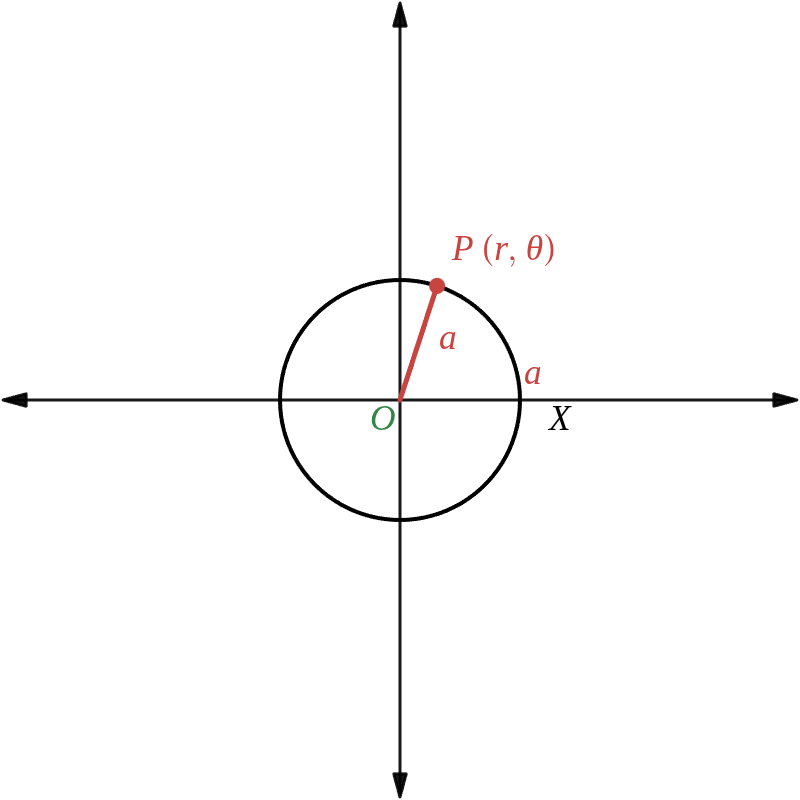
中心が極 \( O \)、半径が \( a \) の円: \(\quad r\ =\ a\)

周上の点 \( P \) の極座標を \( (r,\ \theta) \) とすると
\(\qquad r\ =\ a,\ \theta \) は任意の値
よって、この円の極方程式は
\(\qquad r\ =\ a \)

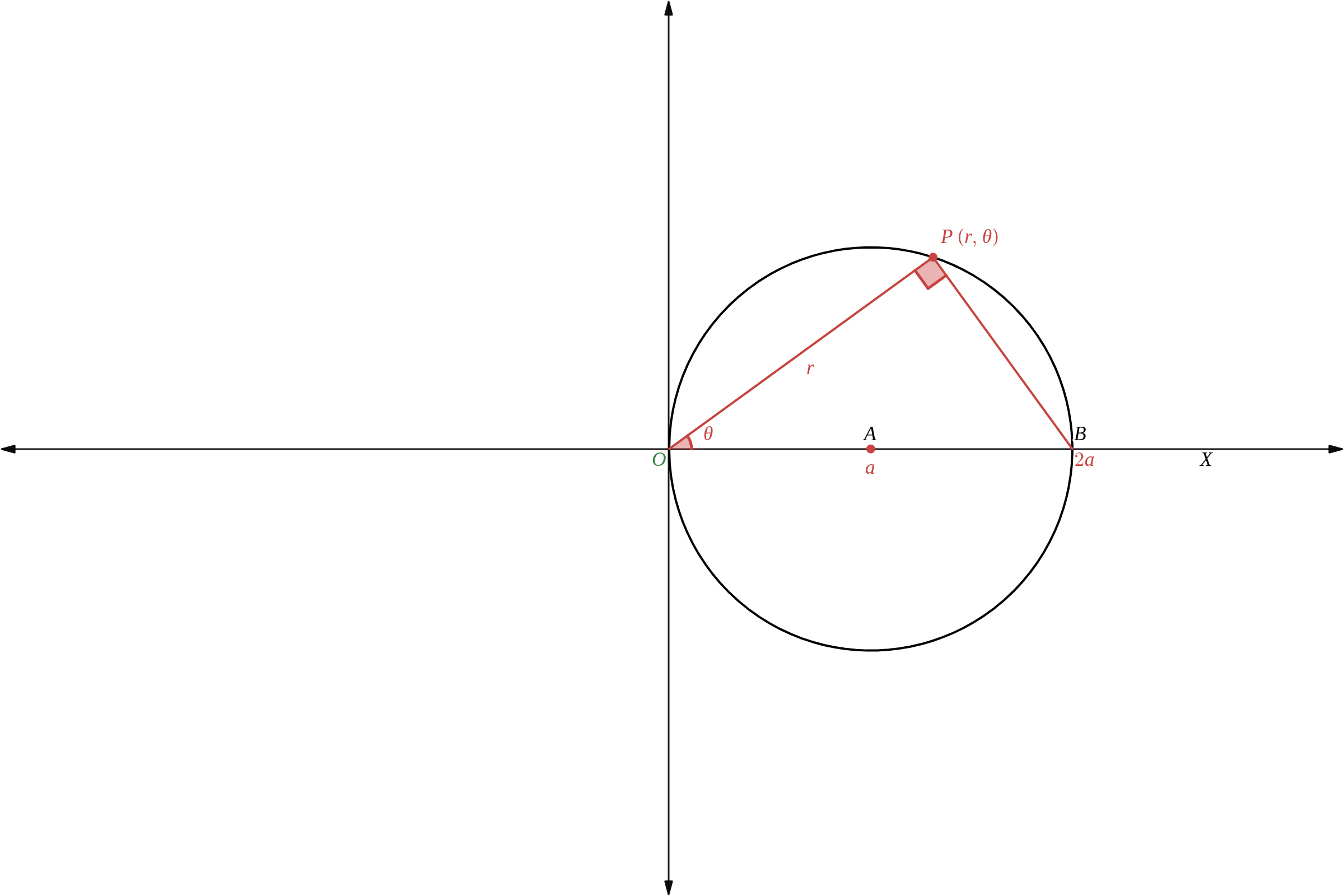
中心 \( A \) の極座標が \( (a, 0) \)、半径が \( a \) の円: \(\quad r\ =\ 2a \cos{\theta} \)

周上の点 \( P \) の極座標を \( (r,\ \theta) \) とすると、
\(\qquad OP\ =\ 2 OA \cos{\angle{AOP}} \)
よって
\(\qquad r = 2a \cos{\theta} \)

※ この極方程式では、\( \cos{\theta} \) は負の値も取りうるから、その場合は \( r\ \lt\ 0 \) となる。

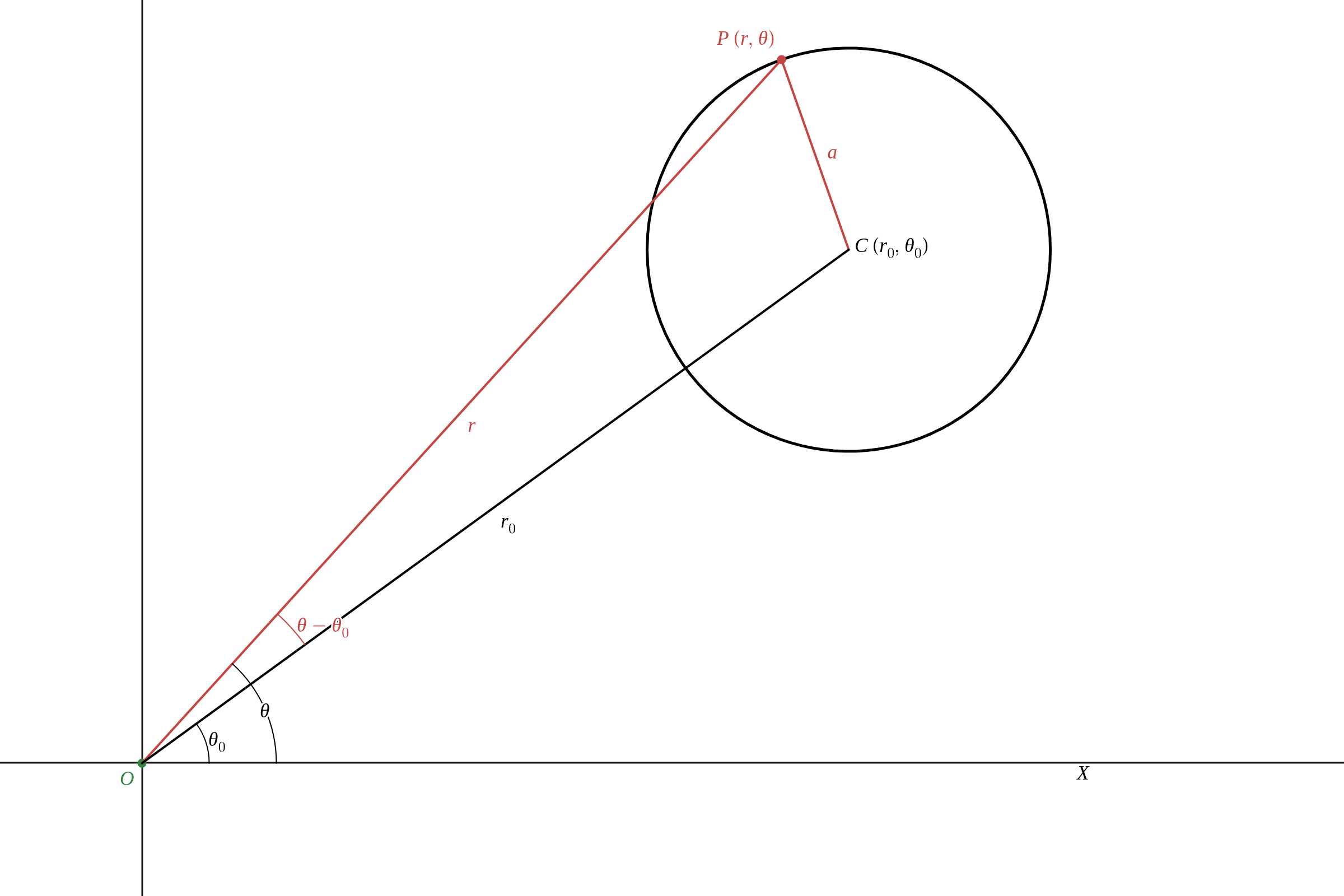
中心 \( C \) の極座標が \( (r_0, \theta_0) \)、半径が \( a \) の円: \(\quad r^2\ -\ 2 r r_0 \cos{ (\theta\ -\ \theta_0) }\ +\ {r_0}^2 =\ a^2 \)

周上の点 \( P \) の極座標を \( (r,\ \theta) \) とする。\( \triangle{OCP} \) において、余弦定理により
\(\displaystyle \qquad {PC}^2\ =\ {OP}^2\ +\ {OC}^2\ -\ 2 OP \cdot OC \cos{ \angle{COP} } \)
よって
\(\displaystyle \qquad a^2\ =\ r^2\ +\ {r_0}^2\ -\ 2 r \cdot r_0 \cos{ (\theta\ -\ \theta_0) } \)
\(\displaystyle \qquad \therefore r^2\ -\ 2 r r_0 \cos{ (\theta\ -\ \theta_0) }\ +\ {r_0}^2 =\ a^2 \)

直線

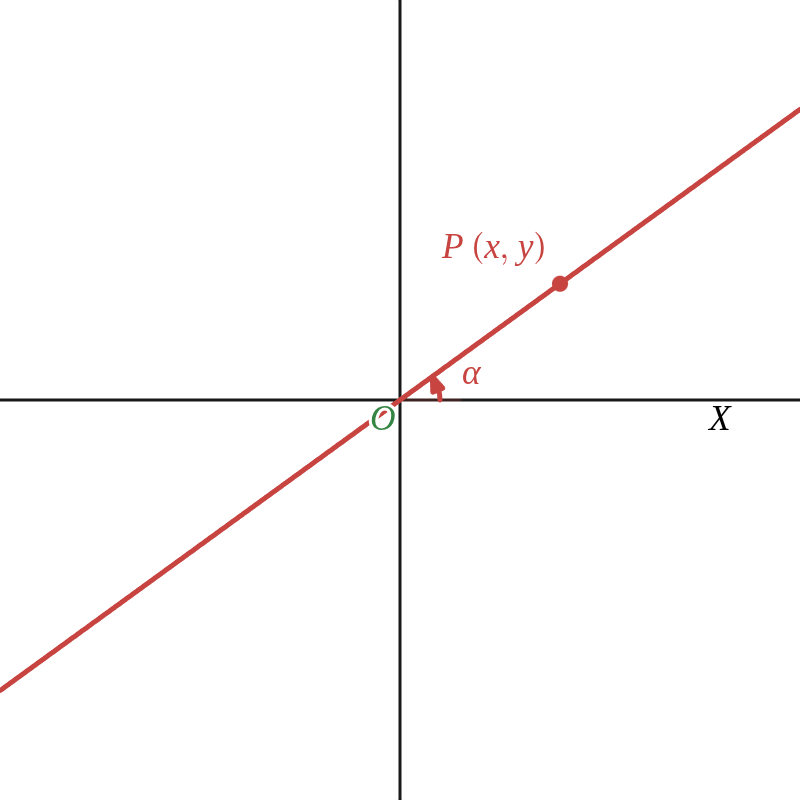
極 \( O \) を通り、視線と \( \alpha \) の角をなす直線: \(\quad \theta\ =\ \alpha \)

直線上の点 \( P \) の極座標を \( (r,\ \theta) \) とすると
\( \qquad r \) は任意の値、\( \theta\ =\ \alpha \)
よって、この直線の極方程式は
\( \qquad \theta\ =\ \alpha \)

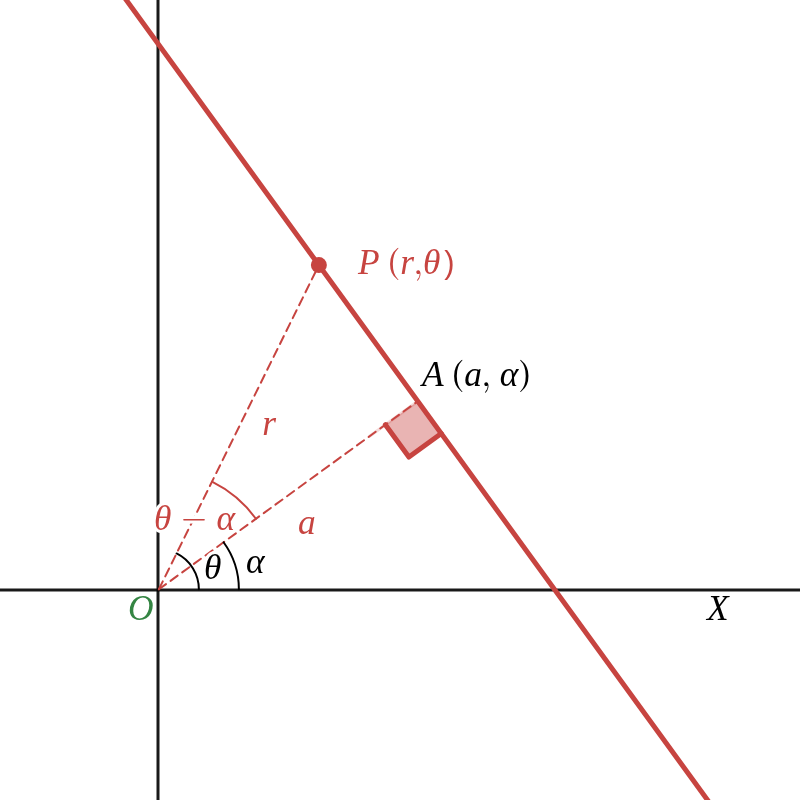
点 \(A (a, \alpha) \) を通り、\( OA \) に垂直な直線: \(\quad r \cos{ (\theta\ -\ \alpha) }\ =\ a\quad (a\ \gt\ 0) \)

直線上の点 \( P \) の極座標を \( (r,\ \theta) \) とすると、極 \( O \) と直線との距離が \( a \) であるから
\(\displaystyle \qquad OA = OP \cos{ \angle{POA} } \)
よって
\(\displaystyle \qquad r \cos{ (\theta\ -\ \alpha) }\ =\ a\quad (a\ \gt\ 0) \)