平均値の定理

関数 \(\ f(x)\ \) が閉区間 \(\ [a,\ b]\ \) で連続、開区間 \(\ (a,\ b)\ \) で微分可能ならば
\(\displaystyle \qquad \dfrac{f(b)\ -\ f(a)}{b\ -\ a}\ =\ f^{\prime}(c),\quad a \lt c \lt b\ \cdots\ (A) \)
を満たす実数 \(\ c\ \) が存在する。

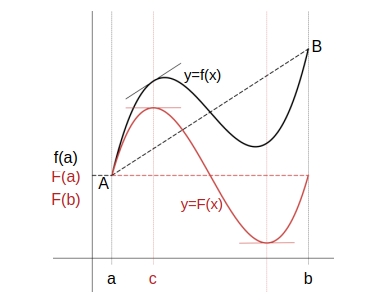
\(\displaystyle \qquad k = \dfrac{f(b)\ -\ f(a)}{b\ -\ a} \cdots ⓵ \)
\(\displaystyle \qquad F(x) = f(x)\ -\ k(x\ -\ a) \)
とする。
閉区間 \(\ [a,\ b]\ \) で \(\ f(x)\ \) が連続のとき、\(\ F(x)\ \) も連続であり、
閉区間 \(\ [a,\ b]\ \) で \(\ f(x)\ \) が微分可能であるとき、\(\ F(x)\ \) も微分可能である。
\(\displaystyle \qquad F(a) = f(a), \)
\(\displaystyle \qquad F(b) = f(b)\ -\ \dfrac{f(b)\ -\ f(a)}{b\ -\ a} (b\ -\ a) = f(a) \)
であるから、\( F(a) = F(b)\quad \) また \(\quad F^{\prime}(x) = f^{\prime}(x)\ -\ k \)
ここで、関数 \(\ F(x) \ \) についてロルの定理により
\(\qquad F^{\prime}(c) = 0, \quad a \lt c \lt b \)
を満たす実数 \( c \) が存在する。
\( F^{\prime}(c) = 0 \) から \(\qquad f^{\prime}(c)\ -\ k = 0 \quad \) すなわち \(\quad f^{\prime}(c) = k \)
よって、\( ⓵ \) から \(\qquad f^{\prime}(c) = \dfrac{f(b)\ -\ f(a)}{b\ -\ a},\ a \lt c \lt b \quad \) を満たす実数 \( c \) が存在する。

関数 \(\ f(x)\ \) が閉区間 \(\ [a,\ a + h]\ \) で連続、開区間 \(\ (a,\ a + h)\ \) で微分可能ならば
\(\displaystyle \qquad f(a + h)\ =\ f(a) + h f^{\prime}(a + \theta h),\quad 0 \lt \theta \lt 1 \)
を満たす実数 \( \theta \) が存在する。

1. の \( (A) \) は
\(\qquad f(b) = f(a) + (b\ -\ a) f^{\prime}(c)\ \cdots\ (B) \)
と言い換えてもよい。
1. で \(\ b\ -\ a = h,\quad \dfrac{c\ -\ a}{b\ -\ a} = \theta\ \) とおくと
\(\displaystyle \qquad b = a + h,\quad c = a + (b\ -\ a)\theta = a + \theta h \)
また、\(\ a \lt c \lt b\quad \) であるから \(\quad 0 \lt c\ -\ a \lt b\ -\ a \)
ゆえに \(\displaystyle \quad 0 \lt \dfrac{c\ -\ a}{b\ -\ a} \lt 1\quad \) すなわち \(\quad 0 \lt \theta \lt 1\)
よって、1. の \( f(x) \) について \( (B) \) から
\(\displaystyle \qquad f(a + h) = f(a) + h f^{\prime}(a + \theta h),\quad 0 \lt \theta \lt 1 \)
を満たす実数 \( \theta \) が存在する。