いろいろな関数の導関数

三角関数の導関数 \(\displaystyle \qquad (\sin{x})’ = \cos{x}, \quad (\cos{x})’ = – \sin{x}, \quad (\tan{x})’ = \frac{1}{\cos^2{x}} \)

\(\displaystyle \begin{eqnarray}
\quad (\sin{x})’ &=& \lim_{h \to 0} \frac{ \sin{(x+h)}\ -\ \sin{x} }{h} \\
&=& \lim_{h \to 0} \dfrac{2 \cos{\left( x + \dfrac{h}{2} \right)} \sin{ \dfrac{h}{2} }}{h} \qquad\qquad \because \sin{A}\ -\ \sin{B} = 2 \cos{ \frac{A + B}{2} } \sin{ \frac{A\ -\ B}{2} } \\
&=& \lim_{h \to 0} \cos{\left( x + \dfrac{h}{2} \right)} \cdot \dfrac{ \sin{ \dfrac{h}{2} } }{ \dfrac{h}{2} } \\
&=& \cos{x} \cdot 1 \qquad\qquad\qquad\qquad\qquad\qquad \because \lim_{x \to 0} \dfrac{ \sin{x} }{x} =1 \\
&=& \cos{x} \\
\end{eqnarray}\)

\(\displaystyle \begin{eqnarray}
\quad (\cos{x})’ &=& \left\{ \sin{ \left( x + \dfrac{\pi}{2} \right) } \right\}’ \\
&=& \cos{ \left( x + \dfrac{\pi}{2} \right) } \\
&=& – \sin{x}
\end{eqnarray}\)

\(\displaystyle \begin{eqnarray}
\quad (\tan{x})’ &=& \left( \dfrac{ \sin{x} }{ \cos{x} } \right)’ \\
&=& \dfrac{ (\sin{x})’ \cos{x}\ -\ \sin{x} (\cos{x})’}{ \cos^2{x} } \\
&=& \dfrac{ \cos^2{x}\ +\ \sin^2{x} }{ \cos^2{x} } \\
&=& \dfrac{ 1 }{ \cos^2{x} } \\
\end{eqnarray}\)

対数関数の導関数

自然対数の底 \( e \) の定義 \(\displaystyle \qquad e = \lim_{h \to 0} (1 + h)^{\frac{1}{h}} \)

\(\displaystyle h \to 0 \) のとき \(\displaystyle (1 + h)^{\frac{1}{h}} \) の極限値 \( (2.71828\cdots) \) を \( e \) で表し、\( \log_e{x} \) を 自然対数 という。
一般に \( \log_e{x} \) は底 \( e \) を省略して \( \log{x} \) と書く。

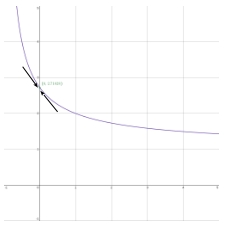
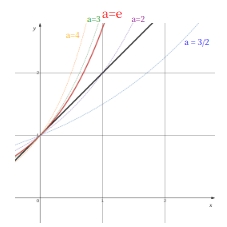
一方、接線の傾きを利用して 曲線 \( y = a^x (a \gt 1) \) 上の点 \( (0, 1) \) における接線の傾きが 1 となるときの \( a \) の値を \( e \) と定める こともできる。すなわち
\(\displaystyle \qquad \lim_{h \to 0} \dfrac{e^h – 1}{h} = 1\)

\( \infty \) に発散する関数の増加の度合い

\(\displaystyle \lim_{x \to \infty}{f(x)} = \infty,\ \lim_{x \to \infty}{g(x)} = \infty \) である２つの関数 \( f(x),\ g(x) \) に関して \(\displaystyle \lim_{x \to \infty}{\dfrac{f(x)}{g(x)}} = \infty \) であるとき \(\ g(x) \ll f(x) \) ［ \(f(x) \) は \( g(x) \) より増加のしかたが急激である］ と表現すると、
\(\qquad \log{x} \ll x^p \ll x^q \ll e^x \qquad (p,\ q\ \) を \( 0 \lt p \lt q \) である定数とする \( ) \)

---

1. \( p \lt q\ \) より \(\ q\ -\ p \gt 0\ \) であるから \(\displaystyle \quad \lim_{x \to \infty}{\dfrac{x^q}{x^p}} = \lim_{x \to \infty}{x^{q – p}} = \infty \)
   すなわち \(\quad x^p \ll x^q \)

2. まず、\(\displaystyle f(x) = e^x\ -\ \left( 1 + x + \dfrac{x^2}{2} \right) \quad (x \gt 0) \quad \) とする。
   \(\qquad f^{\prime}(x) = e^x\ -\ (1 + x) \)
   \(\qquad f^{\prime\prime}(x) = e^x\ -\ 1 \gt 0 \quad (x \gt 0) \)
   よって、\( f^{\prime}(x) \) は増加し、\( f^{\prime}(0) = 0 \) であるから
   \(\qquad f^{\prime}(x) \gt 0 \quad (x \gt 0) \)
   よって、\( f(x) \) は増加し、\( f(0) = 0 \) であるから
   \(\displaystyle \qquad f(x) \gt 0 \quad (x \gt 0) \qquad \therefore e^x \gt 1 + x + \dfrac{x^2}{2} \quad (x \gt 0) \)

   次に、上記より、\( x \gt 0 \) のとき \(\displaystyle \quad e^x \gt \dfrac{x^2}{2} \quad \) すなわち \(\displaystyle \quad \dfrac{e^x}{x} \gt \dfrac{x}{2} \quad \) が成り立つ。
   ここで、\(\displaystyle \lim_{x \to \infty} \dfrac{x}{2} = \infty \) であるから、 \(\displaystyle \quad \lim_{x \to \infty}{\dfrac{e^x}{x}} = \infty \cdots ①\)
   一方、\(\displaystyle \quad \lim_{x \to \infty}{\dfrac{e^x}{x^q}} = \lim_{x \to \infty}{ \left( {\dfrac{e^{\frac{x}{q}}}{x}} \right)^q } = \lim_{x \to \infty}{ \left( {\dfrac{e^{\frac{x}{q}}}{ \dfrac{x}{q} \cdot q }} \right)^q } = \lim_{x \to \infty}{ \left( {\dfrac{e^{\frac{x}{q}}}{ \dfrac{x}{q} }} \right)^q } \cdot \dfrac{1}{q^q} \)
   \(\displaystyle \dfrac{x}{q} = s \) とおくと \( x \to \infty \) のとき \( s \to \infty \) で、①より、\(\displaystyle \qquad \lim_{x \to \infty}{\dfrac{e^x}{x^q}} = \dfrac{1}{q^q} \cdot \lim_{s \to \infty}{\left( \dfrac{e^s}{s} \right)^q} = \infty\)
   すなわち、\(\displaystyle x^q \ll e^x \qquad \) ［\( e^x \) は \( x^q \) より増加の仕方が急激である］

3. \( \log{x} = t\quad \) とおくと \(\quad x = e^t\quad \) で、\(\quad x \to \infty\quad \) のとき \(\quad t \to \infty,\quad pt \to \infty \)
   ① を利用すると、\(\displaystyle \quad \lim_{x \to \infty}{\dfrac{x^p}{log x}} = \lim_{t \to \infty}{\dfrac{(e^t)^p}{t}} = \lim_{t \to \infty}{\dfrac{e^{pt}}{pt} \cdot p} = \infty\)
   すなわち、\(\quad \log{x} \ll x^p \)

<----------------------------------------------------------------->

対数関数の導関数

\( a \gt 0, a \neq 1 \) とする。

\(\displaystyle (\log_{a}{x})’ = \frac{1}{x \log{a}} \)

\(\displaystyle \begin{eqnarray}
\quad (\log_{a}{x})’ &=& \lim_{\Delta x \to 0} \frac{ \log_{a}{(x + \Delta x)}\ -\ \log_{a}{x} }{ \Delta x } \\
&=& \lim_{\Delta x \to 0} { \dfrac{1}{\Delta x} \log_{a}{ \left( 1 + \dfrac{\Delta x}{x} \right) } } \\
&=& \lim_{\Delta x \to 0} { \dfrac{1}{x} \dfrac{x}{\Delta x} \log_{a}{ \left( 1 + \dfrac{\Delta x}{x} \right) } }
\end{eqnarray}\)

\(\displaystyle h = \frac{\Delta x}{x} \) とおくと

\(\displaystyle \begin{eqnarray}
\quad (\log_{a}{x})’ &=& \dfrac{1}{x} \lim_{h \to 0} { \log_{a}{ ( 1 + h)^{\frac{1}{h}} } } \\
&=& \dfrac{1}{x} \log_{a}{e} \\
&=& \dfrac{1}{x \log{a}}
\end{eqnarray}\)

\(\displaystyle (\log {x})’ = \frac{1}{x} \)

\(\displaystyle \quad (\log_{a}{x})’ = \dfrac{1}{x \log{a}} \)
で、特に \( a = e \) のとき
\(\displaystyle \begin{eqnarray}
\quad (\log {x})’ &=& \dfrac{1}{x \log{e}} \\
&=& \dfrac{1}{x}
\end{eqnarray}\)

\(\displaystyle (\log {|x|})’ = \frac{1}{x}, \quad (\log_{a} {|x|})’ = \frac{1}{x \log {a}} \)

\(\quad x \gt 0 \) のとき \(\displaystyle \qquad (\log {|x|})’ = (\log x)’ = \frac{1}{x} \)
\(\quad x \lt 0 \) のとき \(\displaystyle \qquad (\log {|x|})’ = \{\log (- x)\}’ = \frac{1}{- x} \cdot (-1) = \frac{1}{x} \)
ゆえに
\(\displaystyle \quad (\log {|x|})’ = \frac{1}{x} \)

また
\(\displaystyle \quad (\log_{a} {|x|})’ = \left( \frac{\log |x|}{\log a} \right)’ = \frac{1}{\log a} \cdot \frac{1}{x} = \frac{1}{x \log {a}} \)

\( x^\alpha \) の導関数 \( \qquad\qquad \alpha \) が実数のとき \( \quad (x^\alpha)’ = \alpha x^{\alpha – 1} \)

\( y = x^\alpha \) の両辺の自然対数をとると
\(\quad \log y = \alpha \log x \)
両辺を \( x \) で微分して
\(\displaystyle \quad \frac{y’}{y} = \alpha \cdot \frac{1}{x} \qquad\qquad\qquad \because (左辺) = \frac{d(\log{y})}{dx} = \frac{d(\log{y})}{dy} \cdot \frac{dy}{dx} = \frac{1}{y} \cdot y’ \)
よって
\(\displaystyle \quad y’ = \alpha \cdot \frac{1}{x} \cdot x^\alpha = \alpha x^{\alpha – 1} \)

指数関数の導関数\( \qquad\qquad (e^x)’ = e^x, \quad (a^x)’ = a^x \log {a} \quad (a \gt 1,\ a \neq 1 とする。) \)

\( y = a^x \) の両辺の自然対数をとると
\( \quad \log{y} = x \log{a} \)

両辺を \( x \) で微分して
\(\displaystyle \quad \frac{y’}{y} = \log a \qquad\qquad\qquad \because (左辺) = \frac{d(\log{y})}{dx} = \frac{d(\log{y})}{dy} \cdot \frac{dy}{dx} = \frac{1}{y} \cdot y’ \)

したがって
\(\displaystyle \begin{eqnarray}
\quad y’ &=& y \log{a} \\
\quad \therefore (a^x)’ &=& a^x \log{a}
\end{eqnarray}\)

特に、\( a = e \) のとき \( (e^x)’ = e^x \log{e} = e^x \)