三角関数の極限
 極限
極限角の単位が弧度法のとき \(\displaystyle \quad \lim_{x \to 0}{\dfrac{\sin x}{x}}\ =\ 1,\quad \lim_{x \to 0}{\dfrac{x}{\sin x}}\ =\ 1 \)
\( x \to 0 \ \ \) であるから、\( \ \ 0 \ \lt \ | x | \ \lt \dfrac{\pi}{2} \ \ \) としてよい。
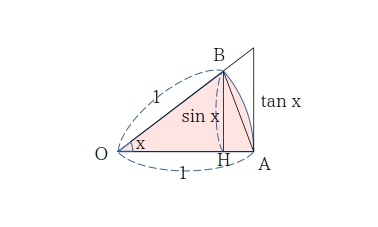
[1] \(\displaystyle \quad 0 \ \lt \ | x | \ \lt \dfrac{\pi}{2} \ \ \) のとき、上の図で、面積について
\( \qquad \triangle OAB \ \lt \ \) 扇形 \( OAB \ \lt \ \triangle OAT \)
ここで \( \quad BH \ \sin{x},\ AT\ =\ \tan{x} \)
また、 \( \quad \) 扇形 \(\displaystyle OAB\ =\ \dfrac{1}{2} \cdot 1^2 \cdot x \)
ゆえに \(\displaystyle \quad \dfrac{1}{2} \cdot 1 \cdot \sin{x}\ \lt\ \dfrac{1}{2} \cdot 1^2 \cdot x\ \lt\ \dfrac{1}{2} \cdot 1 \cdot \tan{x} \qquad \) すなわち \(\qquad \sin{x}\ \lt\ x\ \lt\ \tan{x} \)
よって \(\displaystyle \quad 1\ \lt\ \dfrac{x}{\sin{x}}\ \lt\ \dfrac{1}{\cos{x}} \)
したがって\(\displaystyle \quad 1\ \gt\ \dfrac{\sin{x}}{x}\ \gt\ \cos{x} \)
\(\displaystyle \lim_{x \to +0}{\cos{x}}\ =\ 1 \quad \) であるから \(\displaystyle \quad \lim_{x \to +0}{\dfrac{\sin{x}}{x}}\ =\ 1 \)
[2] \(\displaystyle \quad – \dfrac{\pi}{2}\ \lt\ x\ \lt\ 0\ \ \) のとき、\( x\ =\ -t\ \ \) とおくと \(\displaystyle \quad 0\ \lt\ t\ \lt\ \dfrac{\pi}{2} \)
ゆえに、[1] により、\(\displaystyle \quad \lim_{x \to -0}{\dfrac{\sin{x}}{x}}\ =\ \lim_{t \to +0}{\dfrac{\sin{(- t)}}{- t}}\ =\ \lim_{t \to +0}{\dfrac{\sin{t}}{t}}\ =\ 1 \)
[1], [2] から \(\displaystyle \quad \lim_{x \to 0}{\dfrac{\sin{x}}{x}}\ =\ 1 \)
更に \(\displaystyle \qquad \lim_{x \to 0}{\dfrac{x}{\sin{x}}}\ =\ \lim_{x \to 0}{\dfrac{1}{\dfrac{\sin{x}}{x}}}\ =\ 1 \)
また \(\displaystyle \quad \lim_{x \to 0}{\dfrac{\tan{x}}{x}}\ =\ \lim_{x \to 0}{\dfrac{\sin{x}}{x} \cdot \dfrac{1}{\cos{x}}}\ =\ 1 \cdot 1\ =\ 1 \)