平面の方程式
空間のベクトル一般に、平面 \( \pi \) はその上の1点 \( A (x_0,\ y_0,\ z_0) \) と \( \pi \) に垂直なベクトル
\(\qquad \overrightarrow{n} = (a, b, c) \qquad (\neq 0) \)
によって決まる。
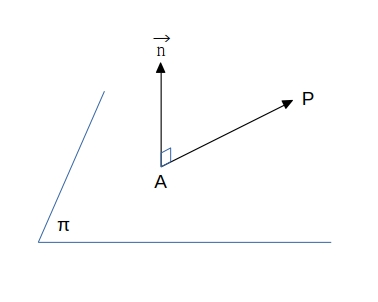
\( \pi \) 上の任意の点を \( P (x,\ y,\ z) \) とすると、\( \overrightarrow{n}\ \perp\ \overrightarrow{AP},\ \overrightarrow{AP} = (x – x_0,\ y – y_0,\ z – z_0)\ \) なので \(\ \overrightarrow{n} \cdot \overrightarrow{AP}\ =\ 0\ \) であるから、平面 \( \pi \) の方程式は
\(\qquad a (x\ -\ x_0)\ +\ b (y\ -\ y_0)\ +\ c (z\ -\ z_0)\ =\ 0 \)
また、\( -(a x_0 + b y_0 + c z_0)\ =\ d \) とすると、
\(\qquad ax\ +\ by\ +\ cz\ +\ d\ =\ 0 \)
となる。
\( \overrightarrow{n} \) を法線ベクトルという。