ド・モアブルの定理
 複素数平面
複素数平面ド・モアブルの定理
\( n \) が整数のとき \( \qquad (\cos{\theta}\ +\ i \sin{\theta})^n\ =\ \cos{n\theta}\ +\ i \sin{n \theta} \)
- 複素数の乗法から、0 でない複素数に \( z\ =\ \cos{\theta}\ +\ i \sin{\theta} \) を掛けると、絶対値は変わらずに偏角は \( \theta \) だけ増える。よって、
\(\displaystyle \qquad (\cos{\theta}\ +\ \sin{\theta})^2\ =\ \cos{2 \theta}\ +\ i \sin{2 \theta} \)
\(\displaystyle \qquad (\cos{\theta}\ +\ \sin{\theta})^3\ =\ \cos{3 \theta}\ +\ i \sin{3 \theta} \)
となり、一般に、自然数 \( n \) について次の等式が成り立つ。
\(\displaystyle \qquad (\cos{\theta}\ +\ \sin{\theta})^n\ =\ \cos{n \theta}\ +\ i \sin{n \theta} \cdots ① \) - 0 でない複素数 \( z \) に対して \( z^0 = 1 \) と定めると、① は \( n\ =\ 0 \) のときも成り立つ。
- 更に、\( z^{-n} = \dfrac{1}{z^n} \) と定めると
\(\displaystyle \begin{eqnarray} \qquad (\cos{\theta}\ +\ i \sin{\theta})^{-n} &=& \dfrac{1}{(\cos{\theta}\ +\ i \sin{\theta})^n} \\
&=& \dfrac{1}{\cos{n \theta}\ +\ i \sin{n \theta}} \\
&=& \dfrac{\cos{n \theta}\ -\ i \sin{n \theta}}{(\cos{n \theta}\ +\ i \sin{n \theta})(\cos{n \theta}\ -\ i \sin{n \theta})} \\
&=& \cos{(n \theta)}\ -\ \sin{(n \theta)} \\
&=& \cos{(-n \theta)}\ +\ \sin{(-n \theta)} \\
\end{eqnarray}\)
以上により、ド・モアブルの定理が成り立つ。
\( 1 \) の \( n \) 乗根
\( n \) は自然数とする。
- \( 1 \) の \( n \) 乗根 (すなわち、方程式 \( z^n\ =\ 1 \) の解) は、次の \( n \) 個の複素数である。
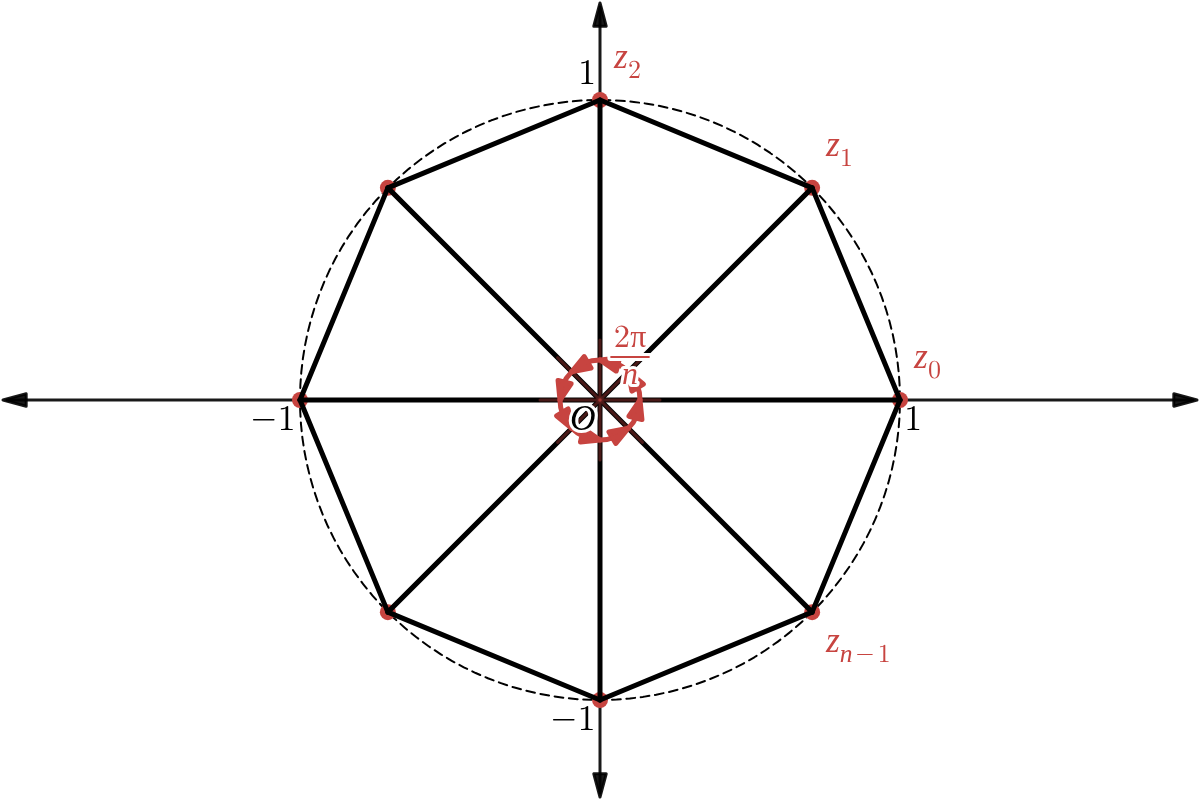
\(\displaystyle \qquad z_k\ =\ \cos{ \dfrac{2 k \pi}{n} }\ +\ i \sin{ \dfrac{2 k \pi}{n} } \qquad (k\ =\ 0,\ 1,\ 2,\ \cdots,\ n-1) \) - \( n\ \geqq\ 3 \) のとき、複素数平面上で \( z_k \) を表す点は 点 \( 1 \) を1つの頂点として単位円に内接する正 \( n \) 角形の各頂点である。
\( z^n\ =\ 1 \qquad \) から \( \qquad |z|^n\ =\ 1 \qquad \) よって \( \qquad |z|\ =\ 1 \qquad \)
ゆえに、\( \qquad z\ =\ \cos{\theta}\ +\ i \sin{\theta} \qquad \) とおくと
\( \qquad z^n\ =\ (\cos{\theta}\ +\ i \sin{\theta})^n\ =\ \cos{n \theta}\ +\ i \sin{n \theta} \)
したがって
\( \qquad \cos{n \theta}\ +\ i \sin{n \theta}\ =\ 1 \)
実部と虚部を比較して
\( \qquad \cos{n \theta}\ =\ 1,\qquad \sin{n \theta}\ =\ 0 \)
よって
\( \qquad n \theta\ =\ 2 \pi \times k \quad \) すなわち \( \quad \theta\ =\ \dfrac{2 k \pi}{n} \quad (k \) は整数 \( ) \)
逆に \( k \) を整数として
\(\displaystyle \qquad z_k\ =\ \cos{ \dfrac{2 k \pi}{n} }\ +\ i \sin{ \dfrac{2 k \pi}{n} } \cdots ①\)
とおくと、\( (z_k)^n\ =\ 1 \) が成り立つから、\( z_k \) は \( 1 \) の \( n \) 乗根である。また、\( z_{n + k} \) と \( z_{k} \) の偏角は \( 2 \pi \) だけ異なり、ともに絶対値は \( 1 \) であるから \( z_{n + k}\ =\ z_{k} \) が成り立つ。
よって、① の \( z_k \) のうち互いに異なるものは \(\ z_0,\ z_1,\ z_2,\ \cdots,\ z_{n-1}\ \) の \( n \) 個である。
なお、\( z^n\ =\ a\ (a\ \gt\ 0) \) の解は \(\ \sqrt[n]{a}\ z_k\ (z_k\ \) は \(\ z^n\ =\ 1\ \) の解 \( ) \) で表される。