複素数と図形
 複素数平面
複素数平面線分の内分点、外分点
- 2点 \( A(\alpha),\ B(\beta) \) を結ぶ線分を \( m:n \) に
- 内分する点を表す複素数は \(\displaystyle \dfrac{n \alpha\ +\ m \beta}{m\ +\ n} \)
- 外分する点を表す複素数は \(\displaystyle \dfrac{-n \alpha\ +\ m \beta}{m\ -\ n} \)
- 特に、中点を表す複素数は \(\displaystyle \dfrac{\alpha\ +\ \beta}{2} \)
- 3点 \( A(\alpha),\ B(\beta),\ C(\gamma)\ \) を頂点とする \( \triangle ABC \) の重心を表す複素数は \(\displaystyle \dfrac{\alpha\ +\ \beta\ +\ \gamma}{3} \)
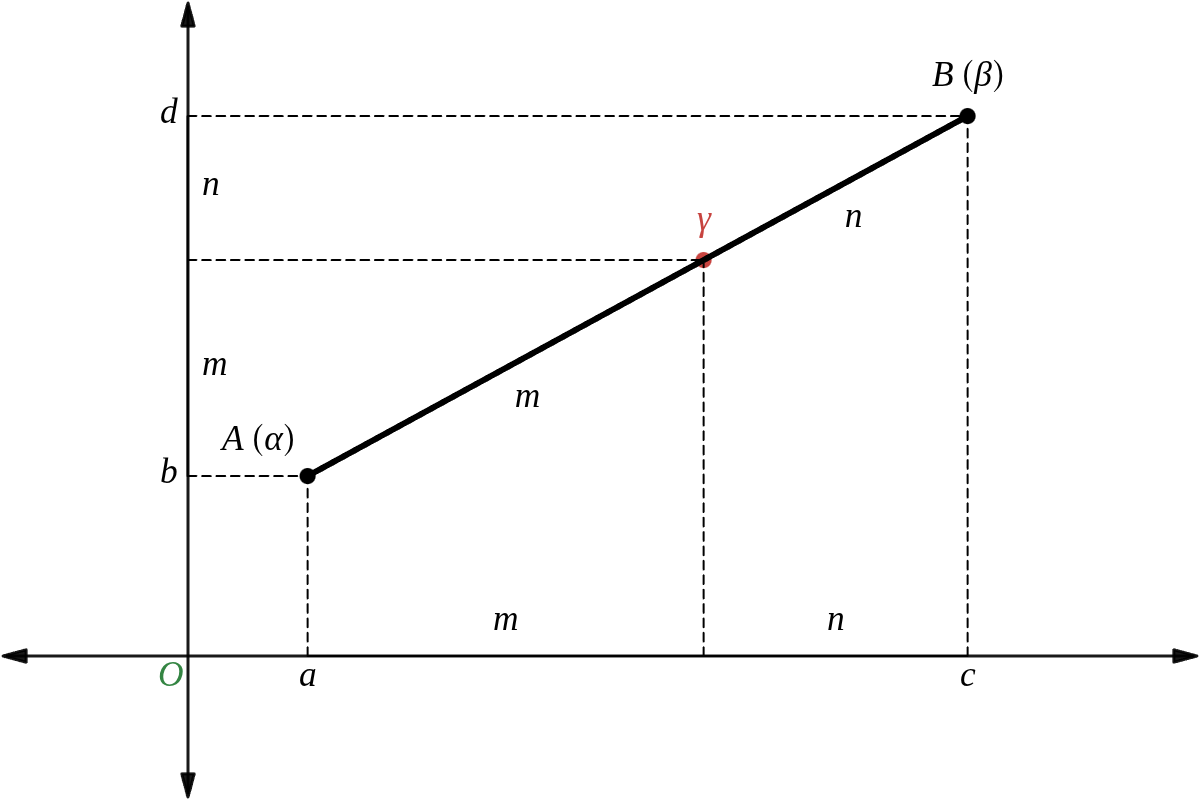
- 2点 \( A(\alpha),\ B(\beta) \) に対して、\(\ \alpha\ =\ a\ +\ bi,\ \beta\ =\ c\ +\ di\ \) とすると、線分 \( AB \) を \( m:n \) に内分する点 \( \gamma \) の実部は \(\displaystyle\ \dfrac{ na\ +\ mc }{ m\ +\ n }\ \)、虚部は \(\displaystyle \ \dfrac{ nb\ +\ md }{ m\ +\ n } \quad \) よって、\(\displaystyle \quad \gamma\ =\ \dfrac{ n \alpha\ +\ m \beta }{ m\ +\ n } \quad \) となる。
外分の場合も同様にして導かれる。
中点については、内分の場合で \( m\ =\ n\ =\ 1\ \) とすると得られる。
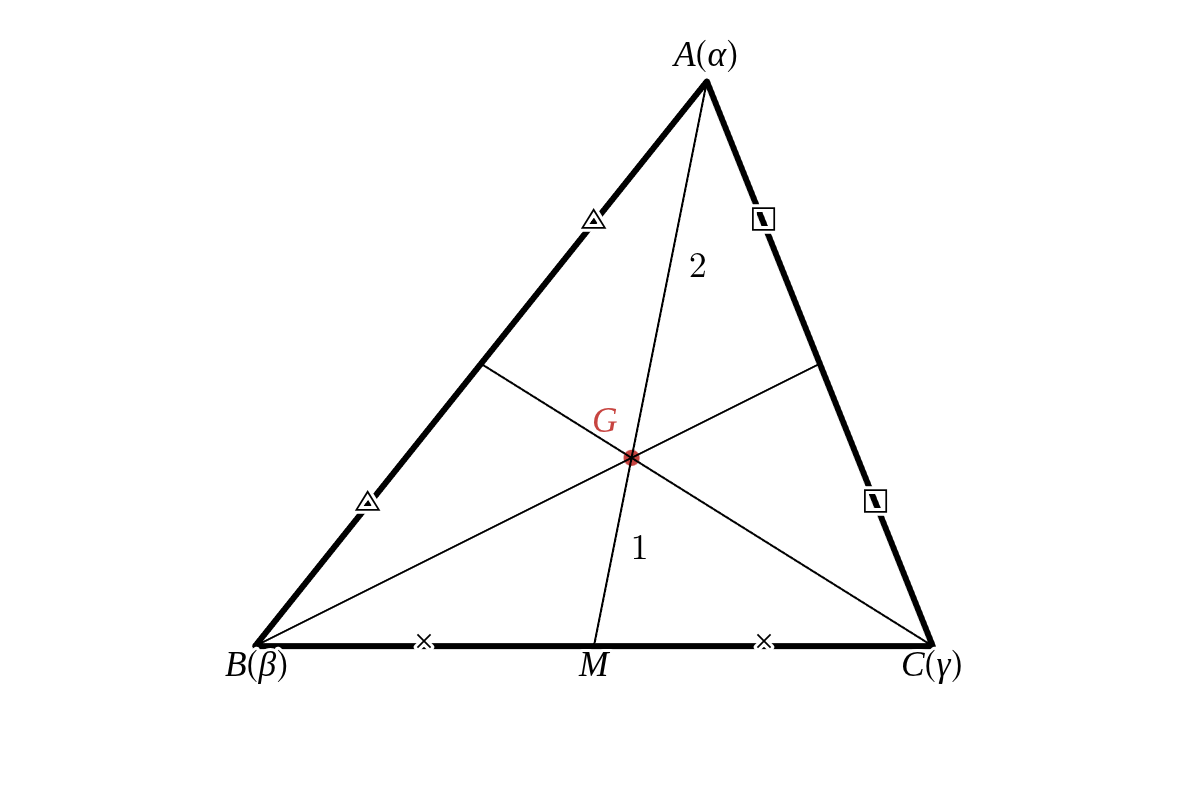
- 3点 \( A(\alpha),\ B(\beta),\ C(\gamma)\ \) を頂点とする \( \triangle ABC \) について、辺 \( BC \) の中点 \( M \) を表す複素数は \(\displaystyle \dfrac{\beta\ +\ \gamma}{2} \)
\( \triangle ABC \) の重心 \( G \) は、線分 \( AM \) を \( 2:1 \) に内分する点であることから重心を表す複素数を導くことができる。
方程式の表す図形
異なる2点 \( A(\alpha),\ B(\beta) \) に対して
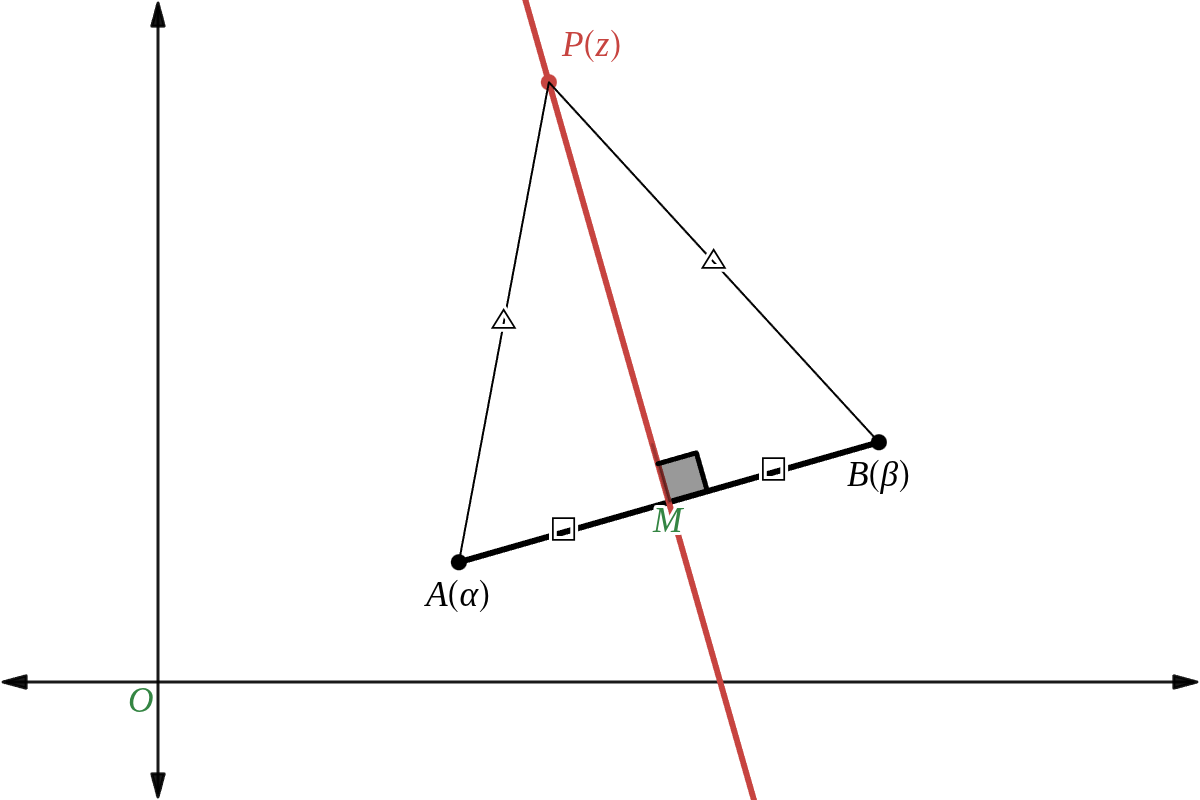
- 方程式 \( |z\ -\ \alpha|\ =\ |z\ -\ \beta| \) を満たす点 \( P(z) \)
- 全体は 線分 \( AB \) の垂直二等分線
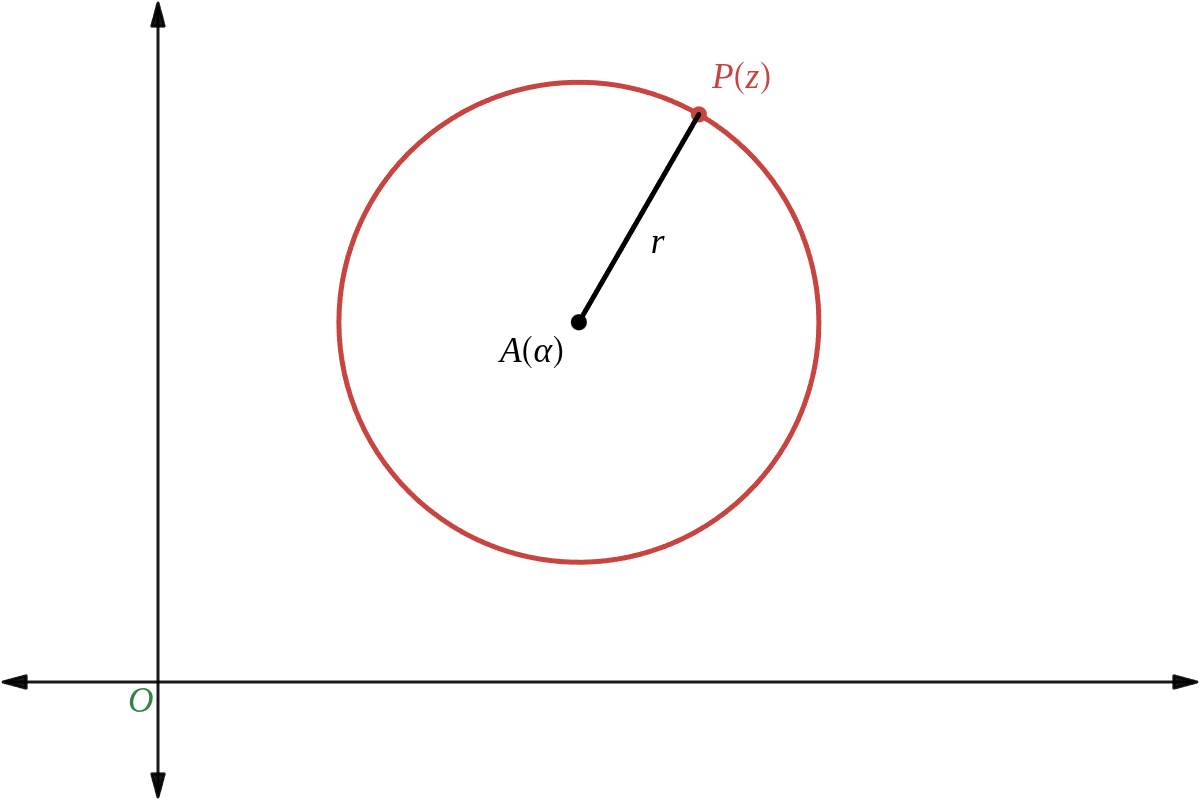
- 方程式 \( |z\ -\ \alpha|\ =\ r \quad (r\ \gt\ 0) \) を満たす点 \( P(z) \)
- 全体は 点 \( \alpha \) を中心とする半径 \( \gamma \) の円
異なる2定点 \( A(\alpha),\ B(\beta) \) と動点 \( P(z),\ r\ (r\ \gt\ 0) \) に対して
\( |z\ -\ a|\ =\ |z\ -\ \beta| \quad \Longleftrightarrow \quad AP\ =\ BP \quad \Longleftrightarrow \quad \) 点 \( P \) は2点 \( A,\ B \) から等距離にある
\( |z\ -\ \alpha|\ =\ r \quad \Longleftrightarrow \quad AP\ =\ r \quad \Longleftrightarrow \quad \) 点 \( P \) は点 \( A \) から \( r \) (一定) の距離にある
アポロニウスの円の利用
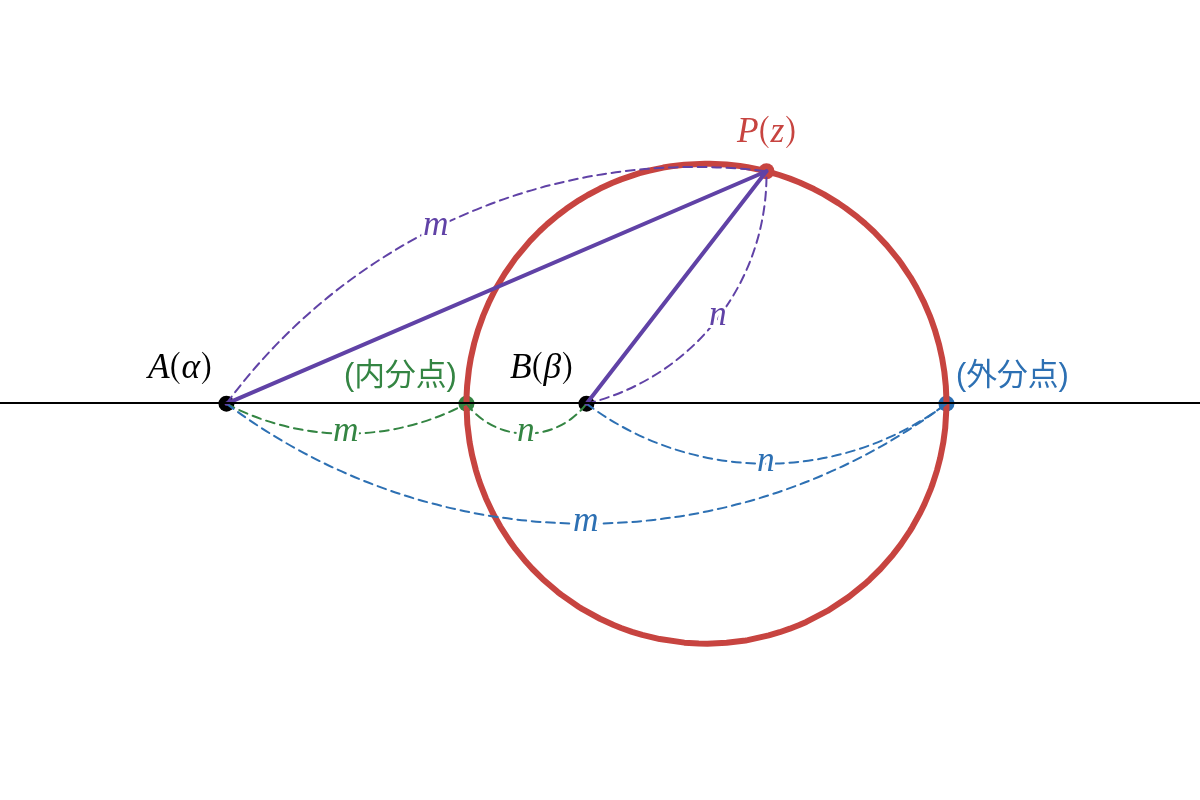
一般に 2定点 \( A,\ B \) からの距離の比が \( m:n\ (m\ \gt\ 0,\ n\ \gt\ 0,\ m\ \neq\ n) \) である点の軌跡は、線分 \( AB \) を \( m:n \) に内分する点と外分する点を直径の両端とする円 (アポロニウスの円) である。
このことを用いると、次のことが成り立つ。
異なる2点を \( A(\alpha),\ B(\beta)\ \) とする。
\( m\ \gt\ 0,\ n\ \gt\ 0,\ m\ \neq\ n \) のとき、方程式 \( n|z\ -\ \alpha|\ =\ m|z\ -\ \beta| \) を満たす点 \( P(z) \) の全体は、線分 \( AB \) を \( m:n \) に内分する点と外分する点を直径の両端とする円 である。
なお、\( m\ =\ n \) のとき、点 \( P \) は線分 \( AB \) の垂直二等分線である。
半直線のなす角、線分の平行・垂直などの条件
異なる4点を \( A(\alpha),\ B(\beta),\ C(\gamma),\ D(\delta)\ \) とし、偏角 \( \theta \) を \( -\pi\ \lt\ \theta\ \leqq \pi \) で考えるとすると
- \( \angle \beta \alpha \gamma\ =\ \arg{ \dfrac{\gamma\ -\ \alpha}{\beta\ -\ \alpha} } \)
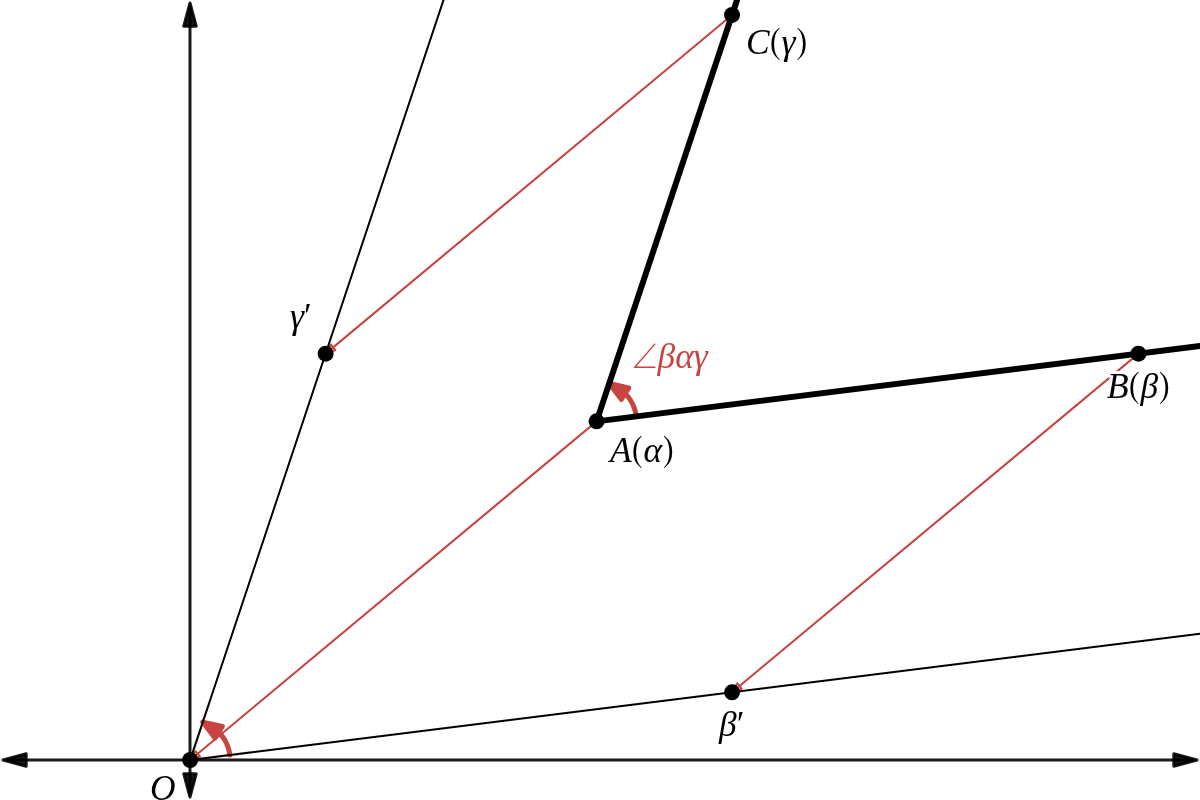
異なる3点 \( A(\alpha),\ B(\beta),\ C(\gamma)\ \) に対し、半直線 \( AB \) から半直線 \( AC \) までの回転角を \( \angle \beta \alpha \gamma \) と表すことにする。
ここで、この角 \( \angle \beta \alpha \gamma \) は向きを含めて考えた角である。すなわち、半直線 \( AB \) から半直線 \( AC \) へ回転する角の向きが反時計周りのとき\( \angle \beta \alpha \gamma \) は正の角、時計回りのとき \( \angle \beta \alpha \gamma \) は負の角となる。また、\( \angle \gamma \alpha \beta\ =\ -\angle \beta \alpha \gamma \) が成り立つ。
点 \( \alpha \) が点 \( O \) に移るような平行移動で点 \( \beta \) が点 \( \beta^\prime \)に、点 \( \gamma \) が点 \( \gamma^\prime \)に移るとすると、
\( \qquad \beta^\prime\ =\ \beta\ -\ \alpha, \quad \gamma^\prime = \gamma\ -\ \alpha \)
よって
\( \qquad \angle \beta \alpha \gamma\ =\ \angle \beta^\prime O \gamma^\prime\ =\ \arg{\gamma^\prime}\ -\ \arg{\beta^\prime} \ =\ \arg{ \dfrac{\gamma^\prime}{\beta^\prime} } \ =\ \arg{ \dfrac{\gamma\ -\ \alpha}{\beta\ -\ \alpha} } \)
- 3点 \( A,\ B,\ C\ \) が一直線上にある \( \quad \Longleftrightarrow \quad \dfrac{ \gamma\ -\ \alpha }{ \beta\ -\ \alpha } \) が実数 [偏角が \( 0 \) または \( \pi \)]
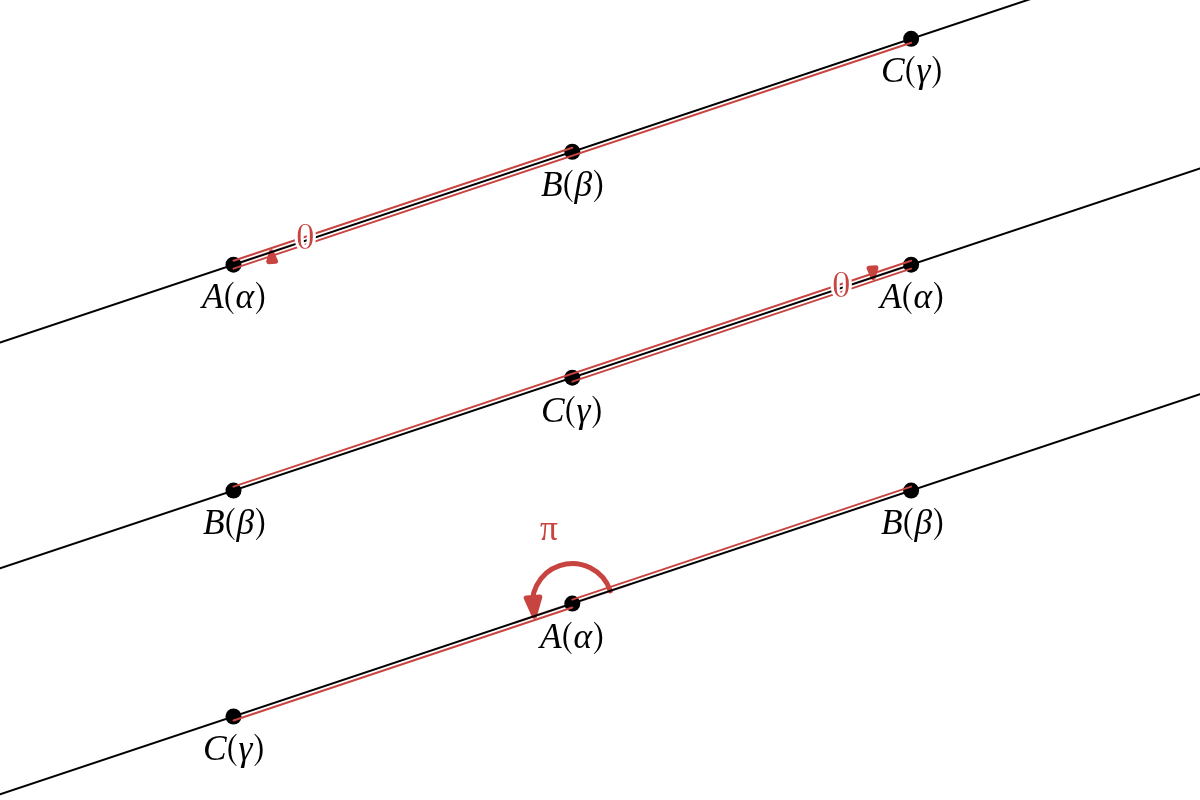
3点 \( A,\ B,\ C\ \) が一直線上にあるとき
\( \qquad \angle \beta \alpha \gamma \ =\ \arg{ \dfrac{\gamma\ -\ \alpha}{\beta\ -\ \alpha} }\ =\ 0,\ \pi\)
偏角が \( 0\ \left( \dfrac{\gamma\ -\ \alpha}{\beta\ -\ \alpha}\ \gt\ 0\right) \) なら \( A,\ B,\ C \) または \( A,\ C,\ B \) の順に一直線上にあり、
偏角が \( \pi\ \left( \dfrac{\gamma\ -\ \alpha}{\beta\ -\ \alpha}\ \lt\ 0\right) \) なら \( B,\ A,\ C \) の順に一直線上にある。
このとき、\( \dfrac{\gamma\ -\ \alpha}{\beta\ -\ \alpha} \) は実数。
- \( AB\ \perp\ AC \quad \Longleftrightarrow \quad \dfrac{ \gamma\ -\ \alpha }{ \beta\ -\ \alpha } \) が純虚数 [偏角が \( \pm \dfrac{\pi}{2} \) ]
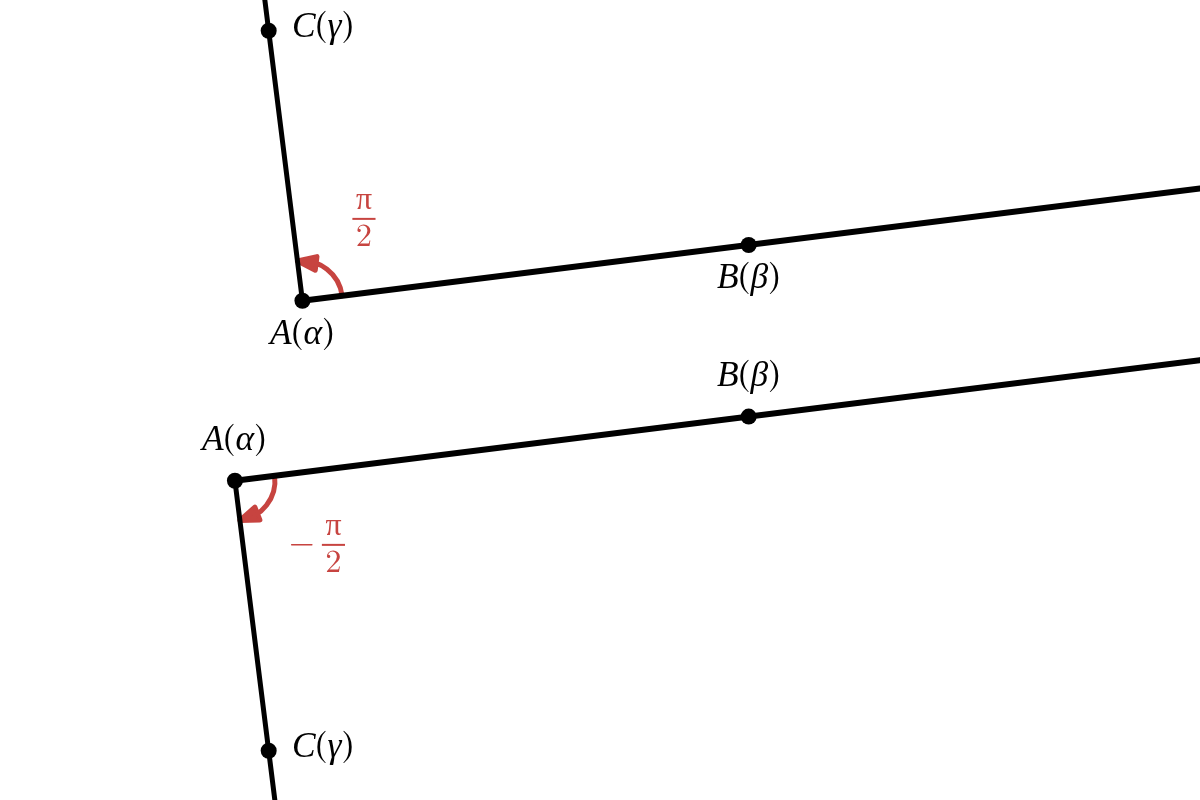
\( AB \perp AC \) であるとき
\( \qquad \angle \beta \alpha \gamma\ =\ \arg{ \dfrac{\gamma\ -\ \alpha}{\beta\ -\ \alpha} }\ =\ \pm \dfrac{\pi}{2} \)
このとき、\( \dfrac{\gamma\ -\ \alpha}{\beta\ -\ \alpha} \) は純虚数。
- \( AB\ /\!/ CD \quad \Longleftrightarrow \quad \dfrac{ \delta\ -\ \gamma }{ \beta\ -\ \alpha } \) が実数、 \( \qquad AB\ \perp CD \quad \Longleftrightarrow \quad \dfrac{ \delta\ -\ \gamma }{ \beta\ -\ \alpha } \) が純虚数
平行移動して 3. に帰着させる。
例えば、垂直の場合は \( \quad C \quad \longrightarrow \quad A \quad \) の平行移動により\( \quad D \quad \longrightarrow \quad D^\prime \quad \) とすると \( \quad D^\prime (\delta\ +\ \alpha\ -\ \gamma) \)
\(\qquad AB\ \perp\ CD \quad\Longleftrightarrow\quad AB\ \perp AD^\prime \quad\Longleftrightarrow\quad \dfrac{ (\delta\ +\ \alpha\ -\ \gamma)\ -\ \alpha }{ \beta\ -\ \alpha}\ =\dfrac{\delta\ -\ \gamma}{\beta\ -\ \alpha} \ \) が純虚数