複素数の極形式と乗法、除法

極形式

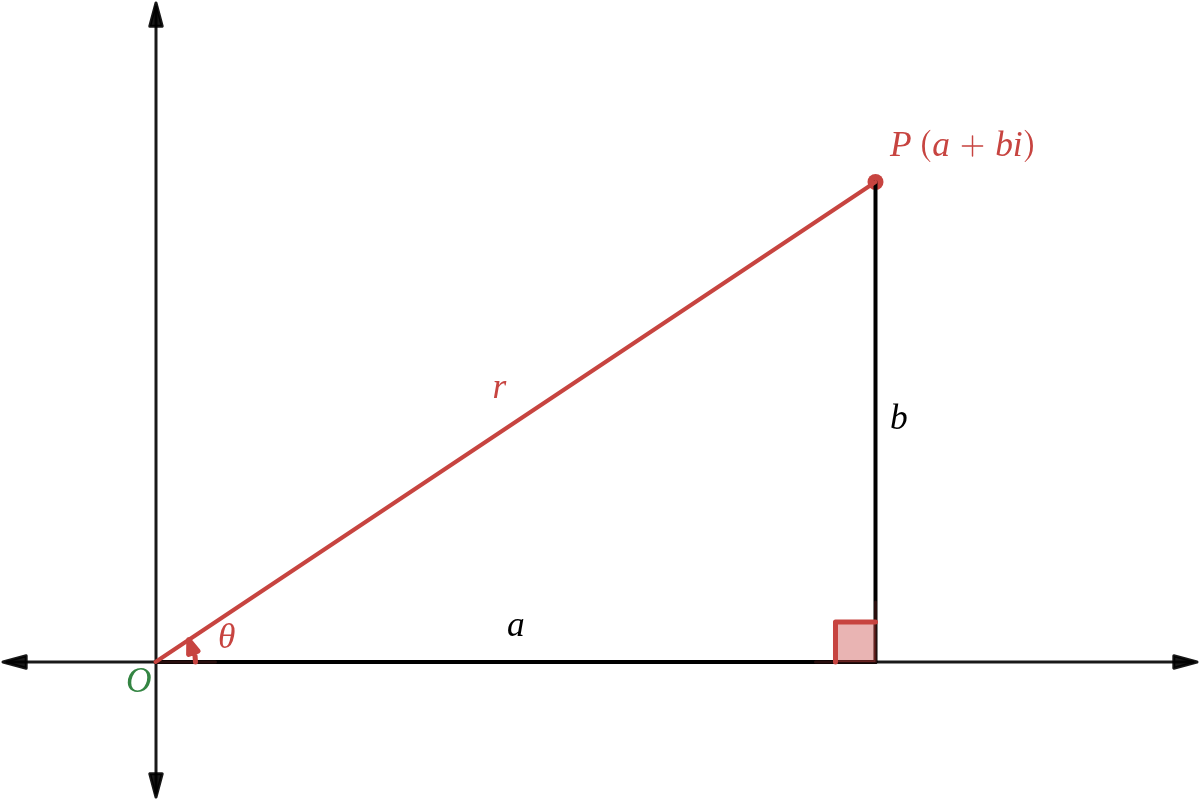
複素数平面上で \( 0 \) でない複素数 \( z\ =\ a\ +\ b i \) を表す点を \( P \) とする。\( OP\ =\ r \)、半直線 \( OP \) を動径と考えて、動径 \( OP \) の表す角を \( \theta \) とすると、\( a\ =\ r \cos{\theta},\ b\ =\ r \sin{\theta} \) であるから
\( \qquad z\ =\ r(\cos{\theta}\ +\ i \sin{\theta}) \quad [r\ \gt\ 0]\quad \cdots① \)
\( ① \) を複素数 \( z \) の 極形式 という。このとき \( r\ =\ |z| \)
また、\( \theta \) を \( z \) の 偏角 といい \( \arg{z} \) で表す。
特に、 \( |z|\ =\ 1\ \)のとき \(\qquad z\ =\ \cos{\theta}\ +\ i \sin{\theta} \)

偏角

記号 \( \arg \) は偏角を表す argument の略である。
極形式で 絶対値 は１通りに定まるが、偏角 は１通りには定まらない。\( \theta \) の代わりに \( \theta\ +\ 2\pi \times n\ \) ( \( n \) は整数) としても、動径が同じ位置に来るからである。
偏角を求めるときは \( 0\ \leqq\ \theta\ \leqq\ 2 \pi \) または \( -\pi\ \leqq\ \theta\ \leqq\ \pi \) の範囲で考えるのが一般的である。

複素数の乗法、除法

\( z_1\ =\ r_1 (\cos{\theta_1}\ +\ i \sin{\theta_1}),\quad z_2\ =\ r_2 (\cos{\theta_2}\ +\ i \sin{\theta_2})\qquad [r_1\ \gt\ 0,\ r_2\ \gt\ 0] \quad \) とする。

複素数 \(\ z_1,\ z_2\ \) の積の極形式

\( z_1 z_2\ =\ r_1 r_2 \{\cos{(\theta_1\ +\ \theta_2)}\ +\ i \sin{(\theta_1\ +\ \theta_2)} \} \)

\( |z_1 z_2|\ =\ |z_1||z_2|,\quad \arg{ (z_1 z_2) }\ =\ \arg{z_1}\ +\ \arg{z_2} \)

---

\(\displaystyle \begin{eqnarray} \qquad z_1 z_2 &=& r_1 (\cos{\theta_1}\ +\ i \sin{\theta_1}) \cdot r_2 (\cos{\theta_2}\ +\ i \sin{\theta_2}) \\
&=& r_1 r_2 \left\{ (\cos{\theta_1} \cos{\theta_2}\ -\ \sin{\theta_1} \sin{\theta_2})\ +\ i (\cos{\theta_1} \sin{\theta_2}\ +\ \sin{\theta_1} \cos{\theta_2}) \right\} \\
&=& r_1 r_2 \left\{ \cos{(\theta_1\ + \theta_2)}\ +\ i \sin{(\theta_1\ + \theta_2)} \right\} \\
\end{eqnarray}\)

複素数 \(\ z_1,\ z_2\ \) の商の極形式

\(\displaystyle \dfrac{z_1}{z_2} =\ \dfrac{r_1}{r_2} \{\cos{(\theta_1\ -\ \theta_2)}\ +\ i \sin{(\theta_1\ -\ \theta_2)} \} \)

\(\displaystyle \left| \dfrac{z_1}{z_2} \right|\ =\dfrac{|z_1|}{|z_2|},\quad \arg{ \dfrac{z_1}{z_2} }\ =\ \arg{z_1}\ -\ \arg{z_2} \qquad (z_2\ \neq\ 0) \)

---

\(\displaystyle \qquad \dfrac{z_1}{z_2}\ =\ z_1 \cdot \dfrac{1}{z_2} \) で、
\(\displaystyle \begin{eqnarray} \qquad\qquad \dfrac{1}{z_2} &=& \dfrac{1}{r_2 (\cos{\theta_2} + i \sin{\theta_2})} \\
&=& \dfrac{ \cos{\theta_2} -\ i \sin{\theta_2} }{r_2 (\cos{\theta_2} + i \sin{\theta_2}) (\cos{\theta_2} -\ i \sin{\theta_2})} \\
&=& \dfrac{ \cos{\theta_2} -\ i \sin{\theta_2} }{r_2 (\cos^2{\theta_2} + \sin^2{\theta_2})} \\
&=& \dfrac{1}{r_2}{ \cos{\theta_2} -\ i \sin{\theta_2} } \\
&=& \dfrac{1}{r_2}\cdot\{ \cos{(-\theta_2)} +\ i \sin{(-\theta_2)} \} \\
\end{eqnarray}\)
\( \qquad \) よって、\( ① \) から
\( \qquad \dfrac{z_1}{z_2}\ =\ \dfrac{r_1}{r_2}\{ \cos(\theta_1\ -\ \theta_2)\ +\ i \sin(\theta_1\ -\ \theta_2) \} \)

偏角についての等式は、両辺の角が \( 2 \pi \) の整数倍の差を除いて一致することを意味する。

複素数の乗法と回転 (複素数の乗法の図形的意味)

複素数平面上で \( P(z) \) とするとき、点 \( r (\cos{\theta}\ +\ i \sin{\theta}) \cdot z \) は、点 \( P \) を原点を中心として角 \( \theta \) だけ回転し、原点からの距離を \( r \) 倍した点 である。

---

\( z\ =\ r_1(\cos{\theta_1}\ +\ i \sin{\theta_1}),\ z^{\prime}\ =\ r(\cos{\theta}\ +\ i \sin{\theta})\cdot z\ \) とし、\( P(z),\ P^{\prime}(z^{\prime})\ \) とする。
複素数の乗法から、
\( \qquad |z^{\prime}|\ =\ r_1 r,\ \arg{z^{\prime}}\ =\ \theta_1\ +\ \theta \)
よって、点 \( P^{\prime}(z^{\prime}) \) は、点\( P \) を原点を中心として角 \( \theta \) だけ回転し、更に原点からの距離を \( r \) 倍した点 である。

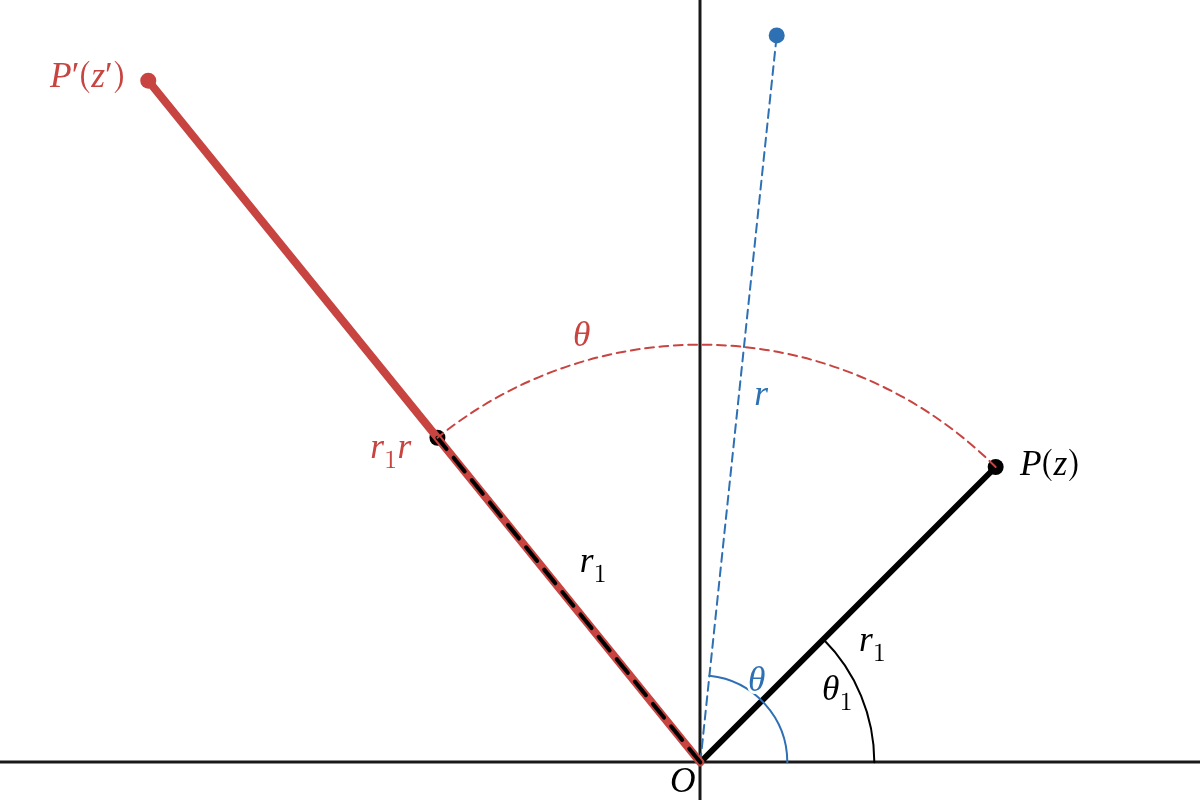
更に、\( iz\ \left(\ =\ 1\left(\cos{\dfrac{\pi}{2}}\ +\ i \sin{\dfrac{\pi}{2}} \right) \cdot z \ \right)\ \) は点 \( z \) を原点を中心として \( \dfrac{\pi}{2} \) だけ回転した点 である。