三角関数の合成

\( a \sin \theta + b \cos \theta = \sqrt {a^2 + b^2} \sin (\theta + \alpha) \)
ただし \( \quad \sin \alpha = \dfrac {b}{\sqrt {a^2 + b^2}} \quad \cos \alpha = \dfrac {a}{\sqrt {a^2 + b^2}} \)

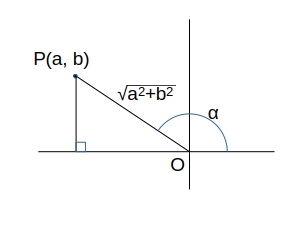
座標が \( (a, b) \) である点を \( P \)、\( OP = r \) とする。
また、線分 \( OP \) が \( x \) 軸の正の向きとなす角を \( \alpha \) とすると、
\( r = \sqrt{a^2 + b^2},\quad a = r \cos \alpha,\quad b = r \sin \alpha \) である。

よって、
\( \begin{eqnarray}
a \sin \theta + b \cos \theta &=& r \cos \alpha \cdot \sin \theta + r \sin \alpha \cdot \cos \theta \\
&=& r (\sin \theta \cdot \cos \alpha + \cos \theta \cdot \sin \alpha )\\
&=& r \sin (\theta + \alpha) \\
&=& \sqrt {a^2 + b^2} \sin (\theta + \alpha)
\end{eqnarray} \)
ただし、\(\quad \sin \alpha = \dfrac {b}{r} = \dfrac {b}{\sqrt {a^2 + b^2}},\quad \cos \alpha = \dfrac {a}{r} = \dfrac {a}{\sqrt {a^2 + b^2}} \)