正規分布

正規分布

連続型確率変数 \( X \) の確率密度関数 \(\displaystyle f(x) = \dfrac{1}{\sqrt{2 \pi}\cdot \sigma} \cdot \epsilon^{- \dfrac{(x – m)^2}{2 \sigma^2}} \) [ \( m, \sigma \) は実数、\( \sigma \gt 0 \)] で与えられるとき、\( X \) は 正規分布 \( N(m, \sigma^2) \) に従う といい、\( y = f(x) \) のグラフを 正規分布曲線 という。

\( X \) が正規分布 \( N(m, \sigma^2) \) に従う確率変数であるとき

• 期待値： \( E(X) = m\)
• 標準偏差： \( \sigma (X) = \sigma \)

\( \epsilon \) (自然対数の底) は無理数で、その値は \( \epsilon = 2.71828\cdots \) である

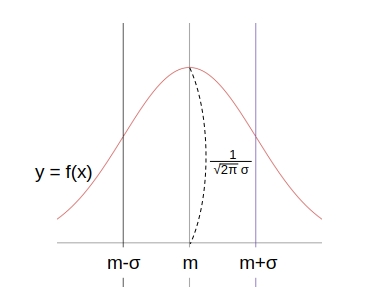
正規分布曲線

正規分布曲線は 連続型確率変数の性質 に加えて次の性質を持つ。

• 曲線は 直線 \( x = m \) (期待値) に関して対称
  \( f(x) \) の値は \( x = m \) で最大で、\( x = m \) から遠ざかるに連れて減少し \(0\) に近づく (\(x\)軸が漸近線)
• 標準偏差 \( \sigma \) が大きくなると曲線は横に広がり山が低くなり、 \( \sigma \) が小さくなると対称軸 \( x = m \) の近くに集中して山が高くなる。

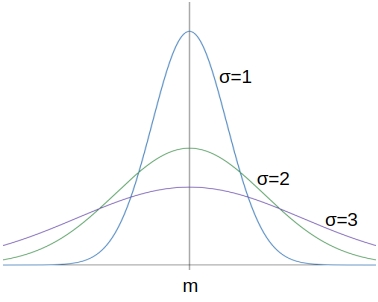
標準正規分布

平均 \(0\)、標準偏差 \(1\) の正規分布 \( N (0, 1) \) を標準正規分布という。
確率変数 \(X\) が正規分布 \( N (m, \sigma^2) \) に従うとき、\(\displaystyle Z = \dfrac{X – m}{\sigma} \) とおくと、確率変数 \(Z\) は 標準正規分布 \( N(0, 1) \) に従う。

\( N (0, 1) \) に従う確率変数 \(Z\) の確率密度関数は \(\displaystyle f(x) = \dfrac{1}{\sqrt{2 \pi}} \cdot \epsilon^{- \dfrac{Z^2}{2}} \) となる。

\( N (0, 1) \) において、確率 \( P(0 \leqq Z \leqq u) \) を \( P(u) \) で表すことにする。
すなわち、\( P(u) = P(0 \leqq Z \leqq u) \) である。正規分布表は種々の \(u\) の値に対する \( P(u) \) の値を評にまとめたものである。

正規分布の標準化

確率変数 \(X\) が正規分布 \( N (m, \sigma^2) \) に従うとき、確率変数 \( aX + b \) ( \(a, b\) は定数) も正規分布に従う確率変数である。

\(\displaystyle Z = \dfrac{ X – m }{ \sigma } \) とすると、

• \(\displaystyle E(Z) = E( \dfrac{X}{\sigma} – \dfrac{m}{\sigma} ) = \dfrac{ E(X) }{ \sigma } – \dfrac{ m }{ \sigma } = 0 \)
• \(\displaystyle V(Z) = V( \dfrac{X}{\sigma} – \dfrac{m}{\sigma} ) = \dfrac{ V(X) }{ \sigma^1 } = 1\)

であり、\(Z\) は標準正規分布 \( N (0, 1) \) に従う。