内分点・外分点

線分上の２点を A (a), B (b) とする。

内分

線分 AB を m:n に内分する点を P (x) とすると、点 P の座標 x は
\( x = \displaystyle \frac{na + mb}{m + n} \)

---

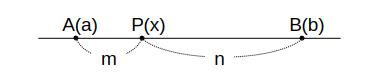
\( \begin{eqnarray}
(x – a):(b – x) &=& m:n \\
m(b – x) &=& n(x – a) \\
mb – mx &=& nx – na \\
x(n + m) &=& na + mb \\
x &=& \displaystyle \frac{na + mb}{m + n}
\end{eqnarray} \)

外分

線分 AB を m:n に外分する点を Q (x) とすると、点 P の座標 x は
\( x = \displaystyle \frac{-na + mb}{m – n} \)

m > n の時

---

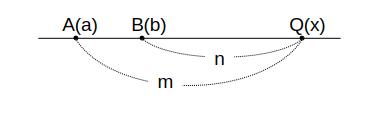
\( \begin{eqnarray}
(x – a):(x – b) &=& m:n \\
m(x – b) &=& n(x – a) \\
mx – mb &=& nx – na \\
x(m – n) &=& -na + mb \\
x &=& \displaystyle \frac{-na + mb}{m – n}
\end{eqnarray} \)

m < n の時

---

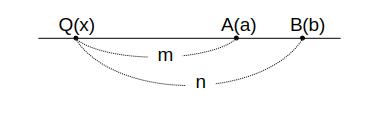
\( \begin{eqnarray}
(a – x):(b – x) &=& m:n \\
m(b – x) &=& n(a – x) \\
mb – mx &=& na – nx \\
x(m – n) &=& -na + mb \\
x &=& \displaystyle \frac{-na + mb}{m – n}
\end{eqnarray} \)