ベクトルの内積

\( \overrightarrow{0} \) でない2つのベクトルを \(\ \overrightarrow{a},\ \overrightarrow{b}\ \) とする。
\(\ \overrightarrow{a}\ =\ \overrightarrow{OA}\ \)、\(\ \overrightarrow{b}\ =\ \overrightarrow{OB}\ \) とするとき、\(\ \angle{AOB}\ =\ \theta\quad(0^\circ\ \leqq\ \theta\ \leqq\ 180^\circ) \ \) を ベクトル \(\ \overrightarrow{a}\ \) と \(\ \overrightarrow{b}\ \) のなす角 という。このとき、積 \(\ |\ \overrightarrow{a}\ |\ |\ \overrightarrow{b}\ |\ cos \theta\ \) を \(\ \overrightarrow{a}\ \) と \(\ \overrightarrow{b}\ \) の 内積 といい、\(\ \overrightarrow{a} \cdot \overrightarrow{b}\ \) で表す。
\(\ \overrightarrow{a} \cdot \overrightarrow{b}\ \) の \(\ \cdot\ \) を省略して \(\ \overrightarrow{a} \ \overrightarrow{b}\ \) と書いてはいけない。また、\(\ \overrightarrow{a} \times \overrightarrow{b}\ \) と書いてもいけない。

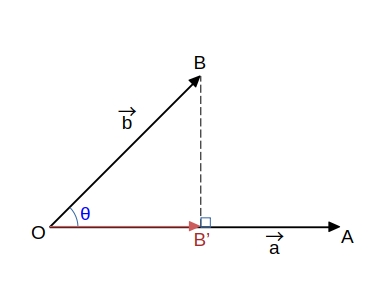
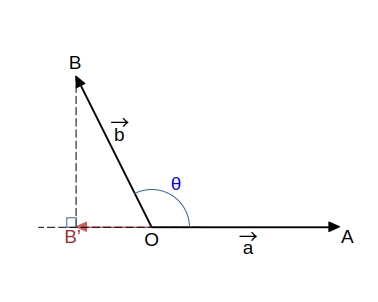
ここで、点 \( B \) から 直線 \( OA \) に垂線 \( BB’ \) をおろしたとき \( \overrightarrow{OA} \) の向きを正として符号をつけた長さ ( \( \overrightarrow{OA} \) と同じ向きの長さは正の数、反対の向きは負の数) を考えると、\(\ OB’\ =\ |\ \overrightarrow{b}\ |\ cos \theta\ \) と表されるから
\(\qquad \overrightarrow{a} \cdot \overrightarrow{b}\ =\ |\ \overrightarrow{a}\ |\ |\ \overrightarrow{b}\ |\ cos \theta\ =\ OA \times OB’ \)
ベクトル \(\ \overrightarrow{OB’}\ \) を \(\ \overrightarrow{OB}\ \) の直線 \( OA \) 上への正射影 という。

\( 0^\circ \leqq \theta \leqq 90^\circ \)	\( 90^\circ \leqq \theta \leqq 180^\circ \)