三角形の重心
 図形と方程式
図形と方程式△ABC の3つの頂点の座標を \( A (x_a, y_a), b (x_b, y_b), C (x_c, y_c), \) とすると 重心 G の座標は
\( G \left(\displaystyle \frac{x_a + x_b + x_c}{3}, \displaystyle \frac{y_a + y_b + y_c}{3} \right) \)
である。
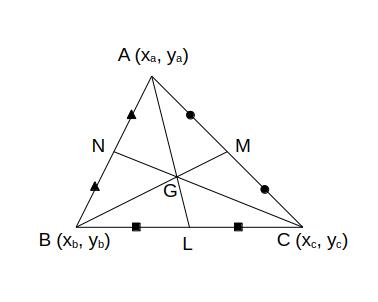
△ABC の 辺BC, 辺CA, 辺AB のそれぞれの中点を L, M, N とすると AL, BM, CN は一点で交わり、その交点 G が △ABC の重心である。
点L は BC の中点なので 点L の座標は
\( \left( \displaystyle \frac{x_b + x_c}{2}, \displaystyle \frac{y_b + y_c}{2} \right) \)
である。重心G は 線分AL を 2:1 に内分する点なので、重心G の座標は
\(
\left( \displaystyle \frac{ 1 \cdot x_a + 2\left( \displaystyle \frac{x_b + x_c}{2} \right) }{2 + 1}, \displaystyle \frac{ 1 \cdot y_a + 2\left( \displaystyle \frac{y_b + y_c}{2} \right) }{2 + 1} \right)
\)
\(
= \left( \displaystyle \frac{x_a + x_b + x_c}{3}, \displaystyle \frac{y_a + y_b + y_c}{3} \right)
\)
\left( \displaystyle \frac{ 1 \cdot x_a + 2\left( \displaystyle \frac{x_b + x_c}{2} \right) }{2 + 1}, \displaystyle \frac{ 1 \cdot y_a + 2\left( \displaystyle \frac{y_b + y_c}{2} \right) }{2 + 1} \right)
\)
\(
= \left( \displaystyle \frac{x_a + x_b + x_c}{3}, \displaystyle \frac{y_a + y_b + y_c}{3} \right)
\)
である。