分数関数

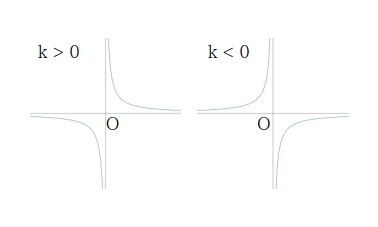
分数関数 \(\displaystyle y = \dfrac{k}{x} \) のグラフ

1. \( x \) 軸、\( y \) 軸 を漸近線とする直角双曲線
2. • \( k \gt 0 \) ならば 第1、3象限
   • \( k \lt 0 \) ならば 第2、4象限

   にそれぞれ存在する。

3. 原点に関して対称

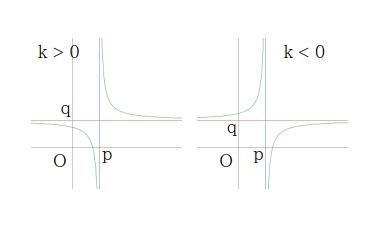
分数関数 \(\displaystyle y = \dfrac{k}{x – p} + q \) のグラフ

1. \( \displaystyle y = \dfrac{k}{x} \) のグラフを \( x \) 軸方向に \( p \)、\( y \) 軸方向に \( q \) だけ平行移動した直角双曲線
2. 漸近線は２直線 \( x = p,\ y = q \)
3. 定義域は \( x \neq p \ \)、値域は \(\ y \neq q \)