サイクロイド
 微分法の応用
微分法の応用\( x \) 軸と原点で接している半径 \( a \) の円が \( x \) 軸上をすべらないように回転するとき、はじめに原点と重なっていた円周上の点 \( P \) が描く軌跡の曲線をサイクロイドという。
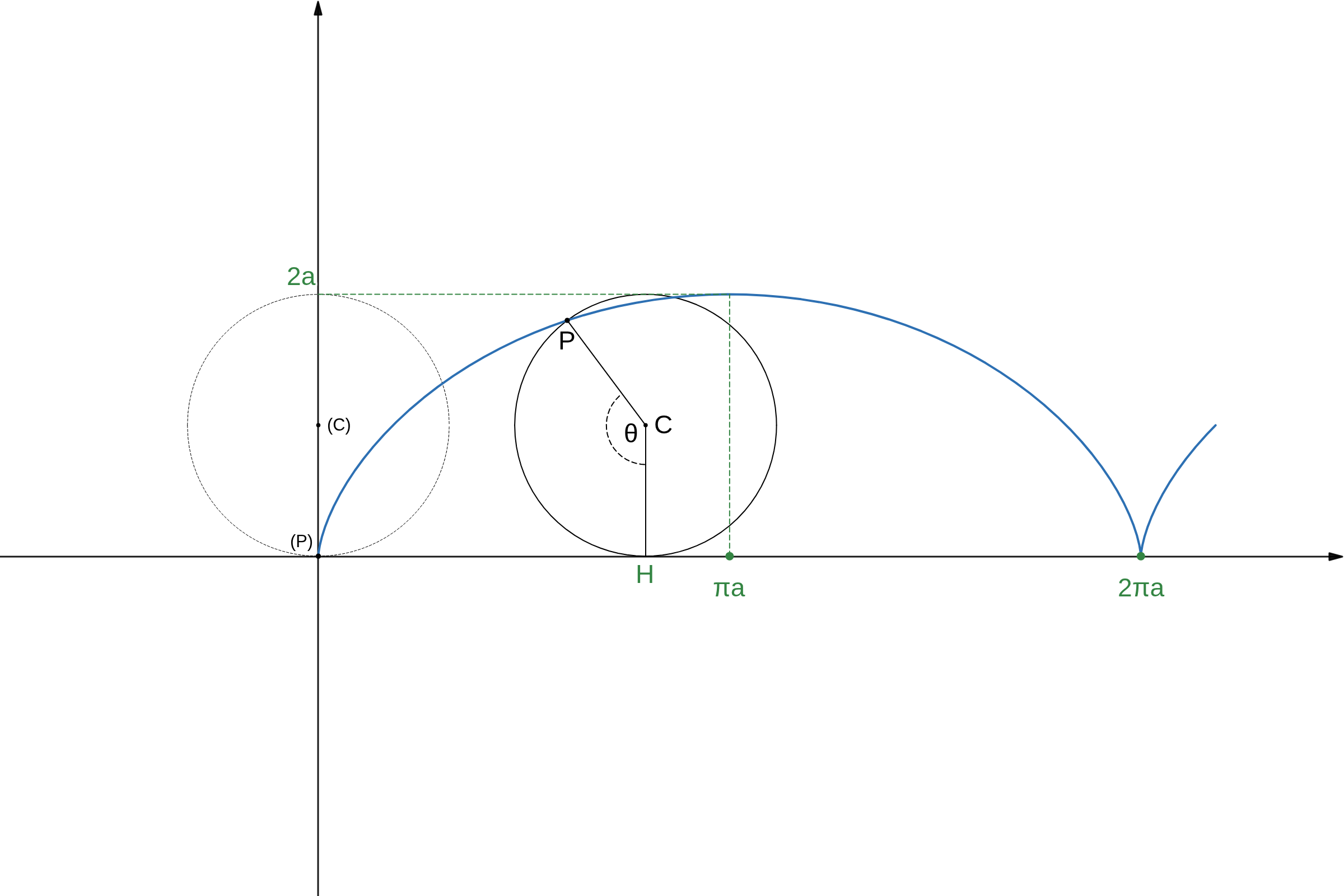
\( \overrightarrow{CP} \) から \( \overrightarrow{CH} \) に至る角を \( \theta \) とすると (\( P \) が原点のときに \( \theta = 0 \) として後は連続的に測る)
\(\qquad \overline{OH}\ =\ \stackrel{\huge\frown}{PH} = a \theta \)
\(\displaystyle \qquad \overrightarrow{CP}\) の方向角 \(\ =\ -\dfrac{\pi}{2}\ -\ \theta \)
これから
\(\displaystyle \begin{eqnarray} \qquad \overrightarrow{OP} &=& \overrightarrow{OC} + \overrightarrow{CP} \\
&=& \begin{pmatrix} a \theta \\ a \end{pmatrix} + a \begin{pmatrix} \cos{ \left( – \dfrac{\pi}{2} – \theta \right) } \\ \sin{ \left( – \dfrac{\pi}{2} – \theta \right) } \end{pmatrix}
&=& \begin{pmatrix} a ( \theta\ -\ \sin{\theta} ) \\ a (1\ -\ \cos{\theta} ) \end{pmatrix}
\end{eqnarray}\)