媒介変数表示
 媒介変数表示
媒介変数表示媒介変数表示
平面上の曲線が1つの変数、例えば \( t \) によって \( \quad x\ = f(t),\quad y\ =\ g(t) \quad \) の形に表されたとき、これをその曲線の 媒介変数表示 または パラメータ表示 といい、\( t \) を 媒介変数または パラメータ という。
2次曲線の媒介変数表示
円 \(\displaystyle \quad x^2\ +\ y^2\ =\ a^2 \)
\(\displaystyle x\ =\ a \cos{\theta},\quad y\ =\ a \sin{\theta} \)
放物線 \(\displaystyle \quad y^2\ =\ 4px \)
\(\displaystyle x\ =\ pt^2,\quad y\ =\ 2pt \)
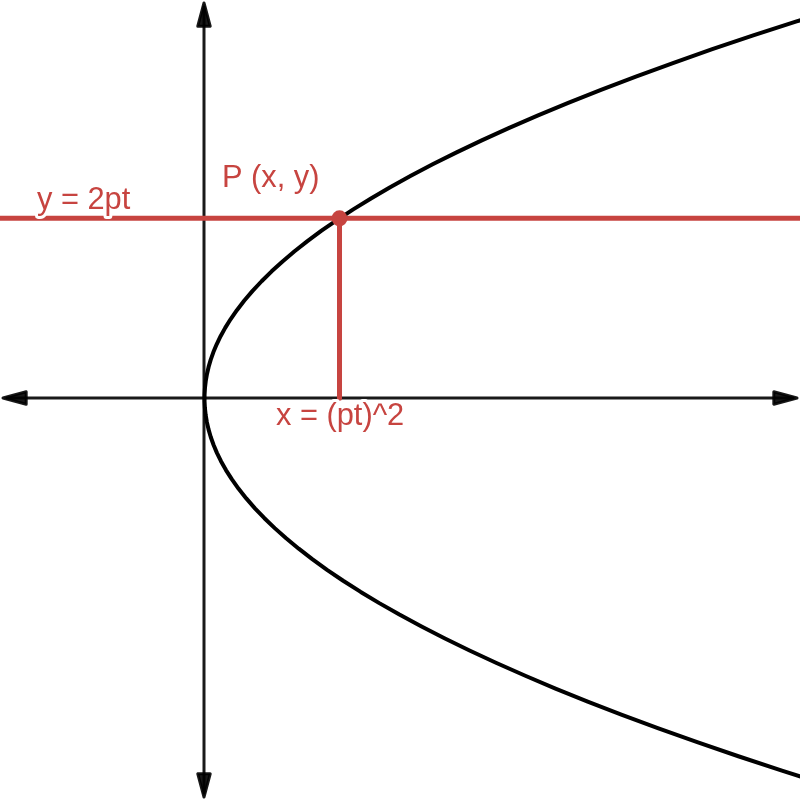
放物線 \( y^2\ =\ 4px \) と、\( x \) 軸に平行な直線群 \( y\ =\ 2pt \) との交点を \( P (x,\ y) \) とすると、\( (2pt)^2\ =\ 4px \) から
\(\qquad x\ =\ pt^2\)
よって
\(\qquad x\ =\ pt^2, \quad y\ =\ 2pt\)
楕円 \(\displaystyle \quad \dfrac{x^2}{a^2}\ +\ \dfrac{y^2}{b^2}\ =\ 1 \)
\(\displaystyle x\ =\ a \cos{\theta},\quad y\ =\ b \sin{\theta} \)
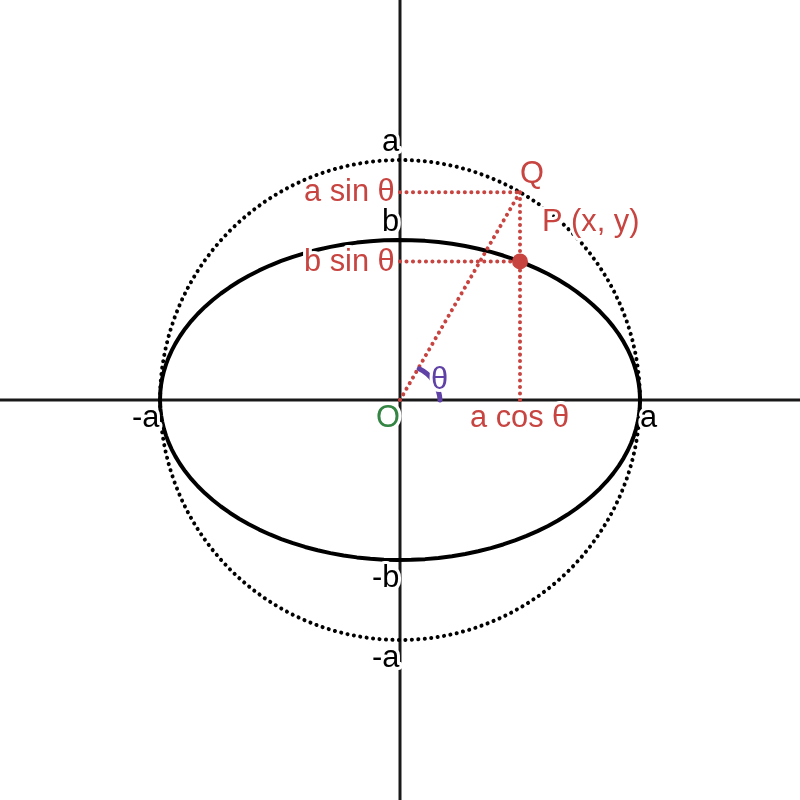
円 \(\quad x^2\ +\ y^2\ =\ a^2,\quad \) 楕円 \(\displaystyle \quad \dfrac{x^2}{a^2}\ +\ \dfrac{y^2}{b^2}\ =\ 1 \quad \) について、楕円は円を \( x \) 軸をもとにして \( y \) 軸方向に \(\displaystyle \dfrac{b}{a} \) 倍に拡大または縮小したものである。
よって、円の周上の点 \( Q (a \cos{\theta},\ a \sin{\theta}) \) に対し、それを \( x \) 軸をもとにして \( y \) 軸方向に \(\displaystyle \dfrac{b}{a} \) 倍した点を \( P (x,\ y) \) とすると、
\(\displaystyle \qquad x\ =\ a \cos{\theta} \)
\(\displaystyle \qquad y\ =\ \dfrac{b}{a} \times a \sin{\theta} = b \sin{\theta} \)
双曲線 \(\displaystyle \quad \dfrac{x^2}{a^2}\ -\ \dfrac{y^2}{b^2}\ =\ 1 \)
\(\displaystyle x\ =\ \dfrac{ a }{ \cos{\theta} },\quad y\ =\ b \tan{\theta} \)
三角関数の相互関係から \(\displaystyle \quad \tan^2{\theta}\ +\ 1\ =\ \dfrac{1}{ \cos^2{\theta} } \quad \) であり、ゆえに \(\displaystyle \quad \dfrac{1}{ \cos^2{\theta} }\ -\ \tan^2{\theta}\ =\ 1 \) であることに注目して、
\(\displaystyle \qquad \dfrac{x}{a} = \dfrac{1}{\cos{\theta}}, \quad \dfrac{y}{b} = \tan{\theta} \)
とおくと、点 \(\displaystyle P \left( \dfrac{a}{\cos{\theta}},\ b \tan{\theta} \right) \) は双曲線 \(\displaystyle \quad \dfrac{x^2}{a^2}\ -\ \dfrac{y^2}{b^2} = 1 \) 上を動くことがわかる。
\(\displaystyle \qquad \because \left( \dfrac{a}{\cos{\theta}} \right)^2 \cdot \dfrac{1}{a^2}\ -\ ( b \tan{\theta} )^2 \cdot \dfrac{1}{b^2}\ =\ \dfrac{1}{ \cos^2{\theta} }\ -\ \tan^2{\theta}\ =\ 1 \)
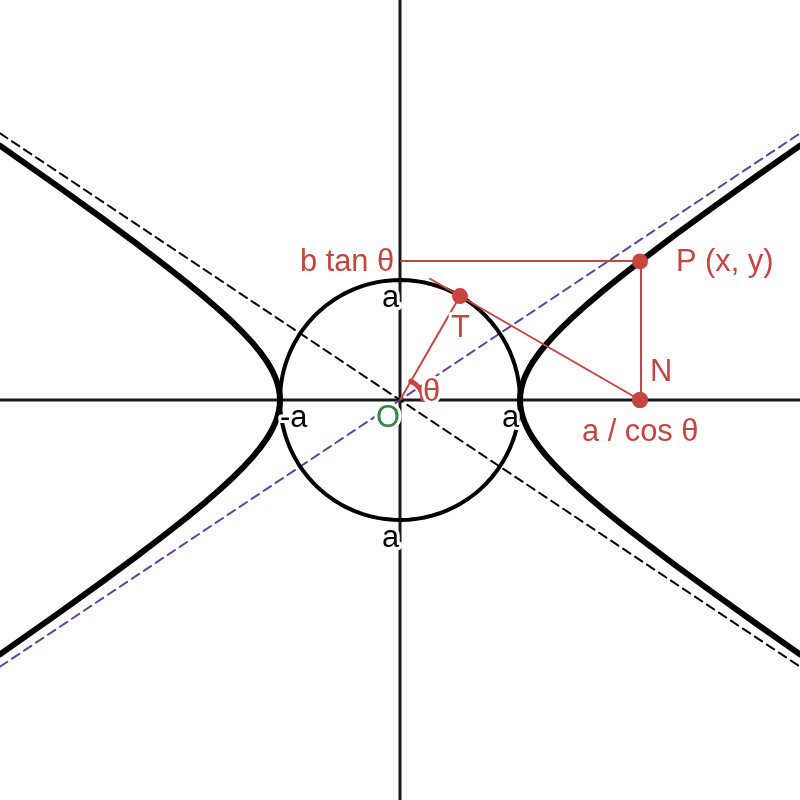
なお、図のように双曲線上の点 \( P (x, y) \) から \( x \) 軸に垂線 \( PN \) を下ろし、\( N \) から \( O \) を中心、半径を \( a \) とする円に接線を引く。このとき、接点を \( T \) とすると、\( \theta \) は動径 \( OT \) の表す角である。
\(\displaystyle \qquad \because \triangle NTO \) において \(\displaystyle ON\ =\ \dfrac{a}{ \cos{\theta} }, OT\ =\ a \) であるから \( \angle TON\ =\ \theta \)
サイクロイド
\(\displaystyle x\ =\ a (\theta\ -\ \sin{\theta}),\quad y\ =\ a (1 -\ \cos{\theta}) \)
円 (半径 \( a \)) が定直線( \( x \) 軸)に接しながら、滑ることなく回転するとき、円周上の定点 \( P \) が描く曲線を サイクロイド という。
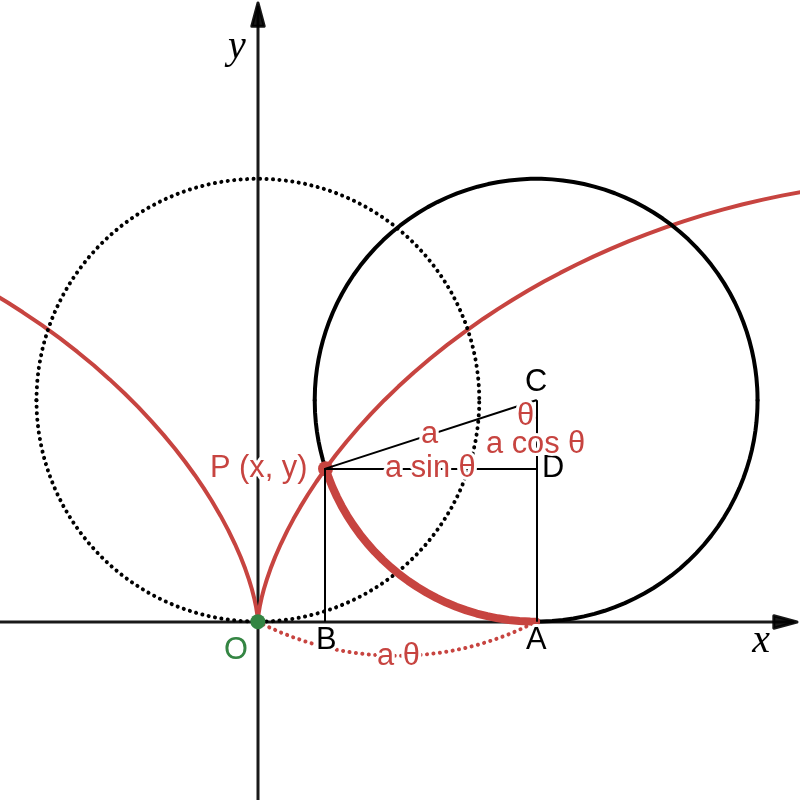
点 \( P \) の最初の位置を原点 \( O \) とし、原点 \( O \) で \( x \) 軸に接する半径 \( a \) の円 \( C \) が角 \( \theta \) だけ回転して、下図のように \( x \) 軸に点 \( A \) で接する位置に来たとき、\( P (x, y) \) とすると
\(\displaystyle \qquad OA\ =\ \overset{\frown}{AP}\ =\ a\theta \)
\(\displaystyle \qquad x\ =\ OB\ =\ OA\ -\ BA\ = a\theta\ -\ a \sin{\theta} \)
\(\displaystyle \qquad y\ =\ BP\ =\ AD\ =\ AC\ -\ DC\ =\ a\ -\ a \cos{\theta}\)
\(\displaystyle \qquad\) すなわち \(\displaystyle \qquad x\ =\ a(\theta\ -\ \sin{\theta}),\quad y\ =\ a(1\ -\ \cos{\theta}) \)
これがサイクロイドの媒介変数表示である。
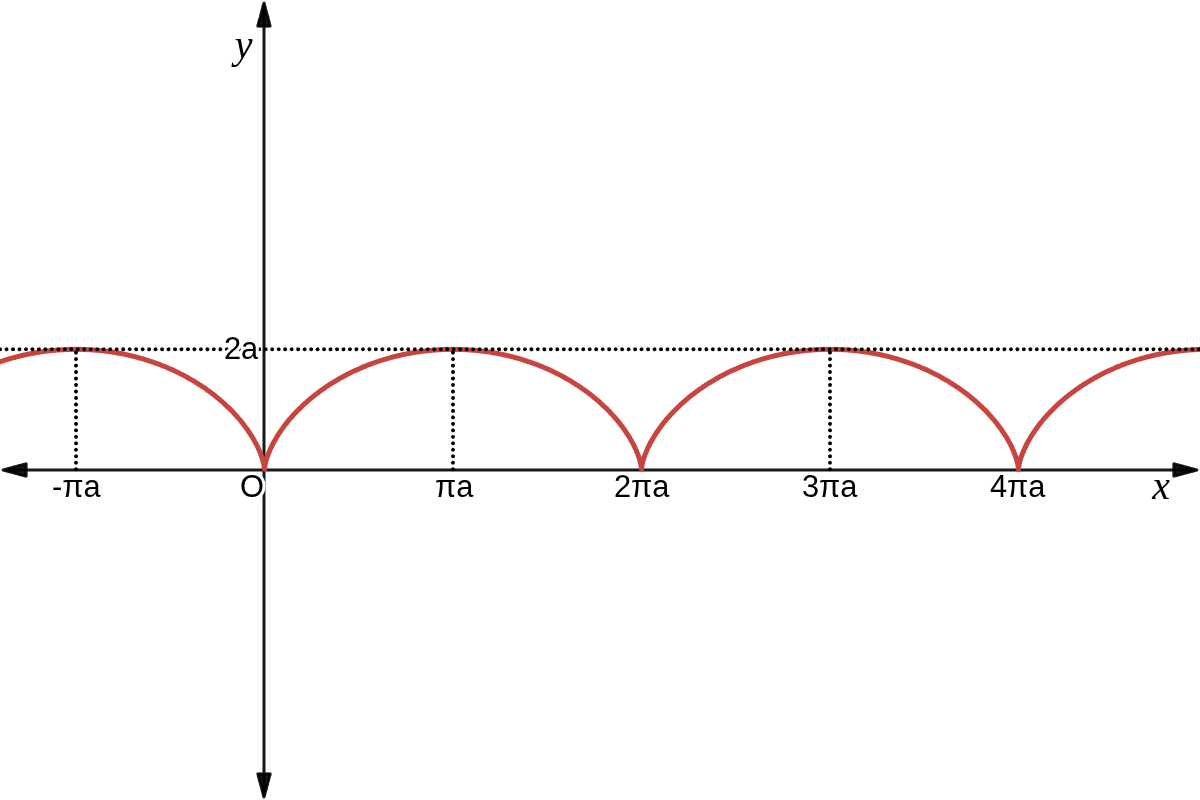
サイクロイドの概形は下図のようになり、\(\quad 0\ \leqq\ x\ \leqq 2 \pi a,\quad 2 \pi a\ \leqq\ x\ \leqq 4 \pi a,\ \cdots \quad \) で同じ形が繰り返される。
媒介教示された曲線の平行移動
曲線 \( x\ =\ f(t),\ y = g(t) \) を \( x \)軸方向に \( p \)、\( y \) 軸方法に \( q \) だけ平行移動した曲線は
\(\qquad x\ =\ f(t)\ +\ p,\quad y\ =\ g(t)\ +\ q \)
で表される。