双曲線

双曲線 \(\displaystyle \quad \dfrac{x^2}{a^2}\ -\ \dfrac{y^2}{b^2} = 1 \quad (a \gt 0,\ b \gt 0) \quad \)［標準形］

1. 中心は 原点、頂点は ２点 \( (a,\ 0),\ (-a,\ 0) \)
2. 焦点は \(\quad F(c,\ 0),\quad F^\prime(-c,\ 0) \quad \) ただし \( \quad c = \sqrt{a^2\ +\ b^2} \)
3. 双曲線は \( x \) 軸、 \( y \) 軸、原点に関して対称。
4. 漸近線は ２直線 \(\displaystyle \quad \dfrac{x}{a}\ -\ \dfrac{y}{b}\ =\ 0,\quad \dfrac{x}{a}\ +\ \dfrac{y}{b}\ =\ 0 \)
5. 双曲線上の任意の点から２つの焦点までの距離の差は \( 2a \) (一定)

---

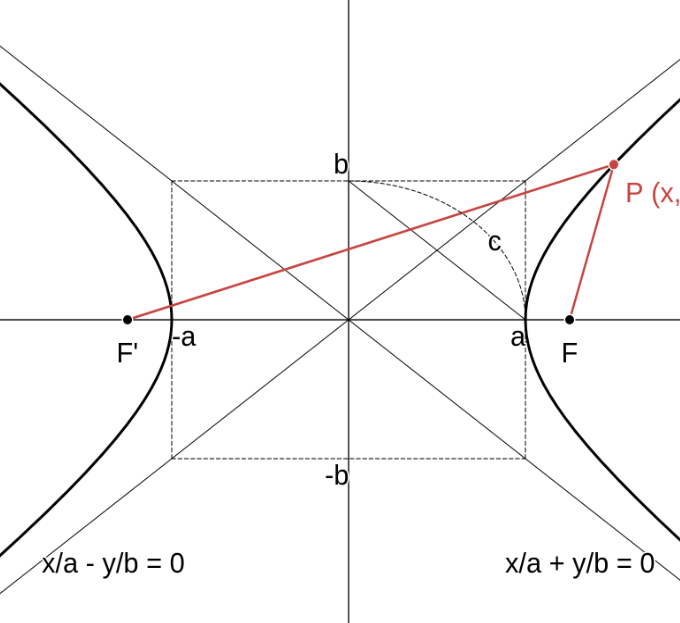
２定点 \( F,\ F^\prime \) からの距離の差が一定 \( (2a) \) である点 \( P \) の軌跡を 双曲線 といい、点 \( F,\ F^\prime \) をその双曲線の 焦点 という。
\( P (x,\ y),\ F(c,\ 0),\ F'(-c,\ 0)\quad [c\ \gt\ a\ \gt\ 0]\quad \) とする。
\( |PF\ -\ PF’| = 2a\ \cdots\ ① \quad\) から \( \qquad \sqrt{(x\ -\ c)^2\ +\ y^2}\ -\ \sqrt{(x\ + c)^2\ +\ y^2}\ =\ \pm 2a \)
楕円の場合と同様に変形すると \(\displaystyle \qquad (c^2\ -\ a^2) x^2\ -\ a^2 y^2\ =\ a^2 (c^2\ -\ a^2) \)
\( b = \sqrt{c^2\ -\ a^2}\ \) (このとき \(\ c\ =\ \sqrt{a^2\ +\ b^2} \ \)) とおいて両辺を \(\ a^2 b^2\ \) で割ると \(\displaystyle \qquad \dfrac{x^2}{a^2}\ -\ \dfrac{y^2}{b^2}\ =\ 1 \cdots ② \qquad \) が導かれる

焦点が \( y \) 軸上にある双曲線 \(\displaystyle \quad \dfrac{x^2}{a^2}\ -\ \dfrac{y^2}{b^2} = -1 \quad (a \gt 0,\ b \gt 0) \)

1. 中心は 原点、頂点は ２点 \( (0,\ b),\ (0,\ -b) \)
2. 焦点は \(\quad F(0,\ c),\quad F^\prime(0,\ -c) \quad \) ただし \( \quad c = \sqrt{a^2\ +\ b^2} \)
3. 双曲線は \( x \) 軸、 \( y \) 軸、原点に関して対称。
4. 漸近線は ２直線 \(\displaystyle \quad \dfrac{x}{a}\ -\ \dfrac{y}{b}\ =\ 0,\quad \dfrac{x}{a}\ +\ \dfrac{y}{b}\ =\ 0 \)
5. 双曲線上の任意の点から２つの焦点までの距離の差は \( 2b \) (一定)

---

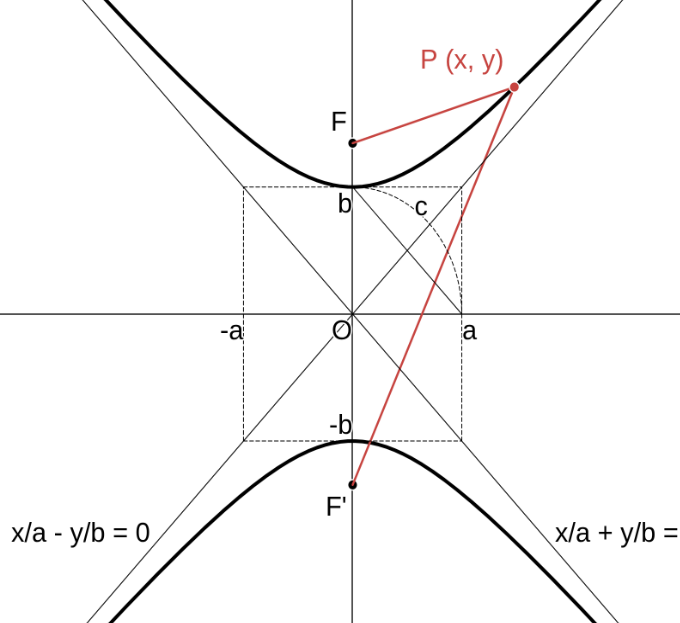
\( c\ \gt\ b\ \gt\ 0\ \) のとき、２定点 \(\ F (0,\ c),\ F^\prime (0, -c)\ \) を焦点とし、この２定点からの距離の差が一定 \( (2b) \) である双曲線の方程式は、標準形と同様に考えて \(\ a = \sqrt{c^2\ -\ b^2}\ \) と置くと \(\ a > 0\ \) で \(\displaystyle \dfrac{x^2}{a^2}\ -\ \dfrac{y^2}{b^2}\ =\ -1\ \) となる。