２次曲線の離心率と準線

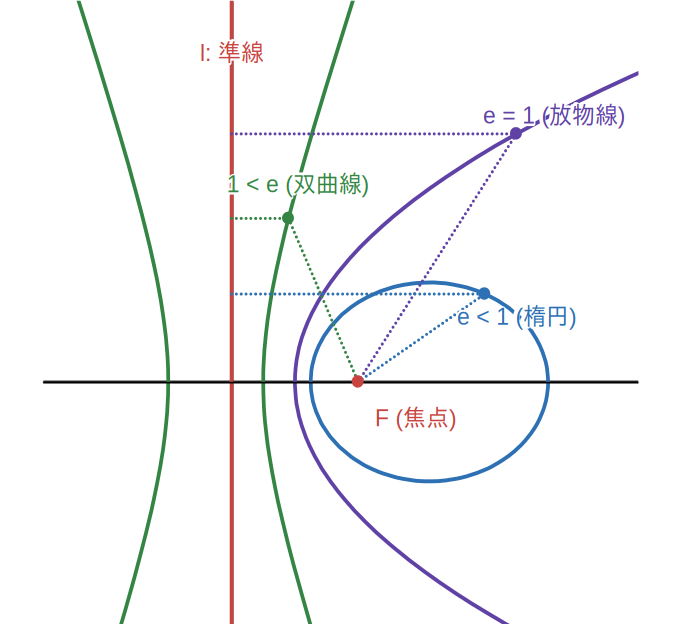
楕円・双曲線も放物線と同じように 定点 \( F \) と \( F \) を通らない定直線 \( l \) からの距離の比が一定である点の軌跡 として定義できる。すなわち、点 \( P \) から \( l \) に引いた垂線を \( PH \) とするとき、 \( PF:PH\ =\ e:1 \) ( \( e \) は正の定数) を満足する点 \( P \) の軌跡は、 \( F \) を１つの焦点とする２次曲線で、 \( l \) を 準線、\( e \) を２次曲線の 離心率 という。
このとき、 \( e \) の値によって、２次曲線は次のように分類される。

• \( 0\ \lt\ e\ \lt\ 1\ \) のとき \( \quad \) 楕円
• \( e\ =\ 1\ \) のとき \( \quad \) 放物線
• \( 1\ \lt\ e\ \) のとき \( \quad \) 双曲線

---

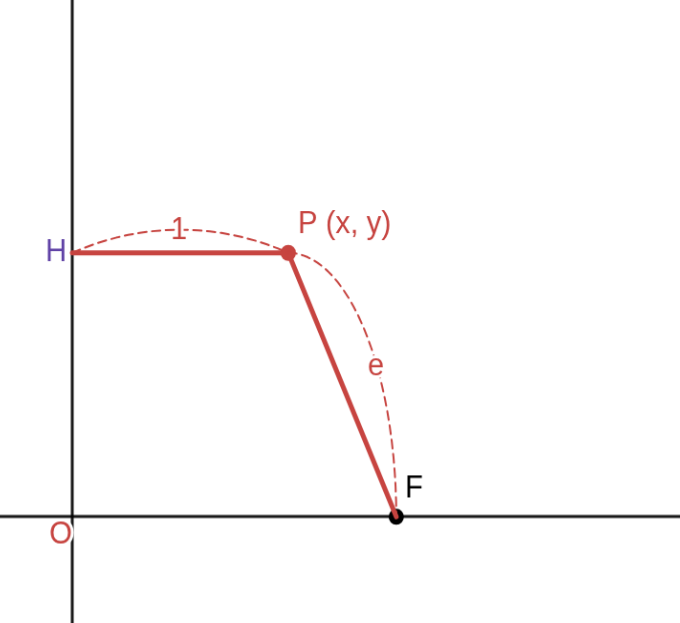
座標平面上で \( l \) を \( y \) 軸 \( (x = 0) \)、\( F (c, 0)\ (c \gt 0) \)、\( P (x，y) \) とし、\( P \) から \( y \) 軸に引いた垂線を \( PH \) とすると
\(\displaystyle \qquad \dfrac{PF}{PH} = \dfrac{ \sqrt{(x\ -\ c)^2 + y^2} }{ |x| } = e \qquad \qquad \therefore\ \sqrt{(x\ -\ c)^2 + y^2}\ =\ e|x| \)
両辺を平方して整理すると
\(\displaystyle \qquad (1\ -\ e^2)x^2\ -\ 2cx\ +\ y^2\ +\ c^2\ =\ 0 \cdots ①\)

1. \(\quad e\ =\ 1 \) のとき

   ① から、\(\displaystyle \qquad y^2 = 2c \left( x\ -\ \dfrac{c}{2} \right) \cdots ② \)
   曲線 ②、\( \quad \) 焦点 \( F (c, 0) \)、\(\quad l: x = 0 \) を \(\quad x \) 軸方向にそれぞれ \(\displaystyle -\dfrac{c}{2} \) だけ平行移動して \( c = 2p \) とおくと
   \(\displaystyle \qquad y^2 = 4px,\quad F (p, 0),\quad l: x = -p \quad \) となる。

2. \(\quad e\ \neq\ 1 \) のとき

   ① から、\(\displaystyle \qquad (1\ -\ e^2) \left( x\ -\ \dfrac{c}{1\ -\ e^2} \right)^2 + y^2 = \dfrac{(ce)^2}{1\ -\ e^2} \cdots ③ \)
   曲線 ③、\( \quad \) 焦点 \( F (c,\ 0) \)、\(\quad l: x = 0 \) を \(\quad x \) 軸方向にそれぞれ \(\displaystyle -\dfrac{c}{1\ -\ e^2} \) だけ平行移動すると
   \(\displaystyle \qquad (1\ -\ e^2)x^2\ +\ y^2 = \dfrac{ (ce)^2 }{1\ -\ e^2},\quad F \left(\dfrac{-ce^2}{1\ -\ e^2},\ 0\right),\quad l: x = -\dfrac{c}{1\ -\ e^2} \cdots ④ \)

   1. \(\quad 0\ \lt\ e\ \lt\ 1\ \) のとき

      \(\displaystyle a\ =\ \dfrac{ce}{1\ -\ e^2} \cdots\ ⑤, \quad b\ =\ \dfrac{ce}{\sqrt{1\ -\ e^2}}\ \cdots\ ⑥\quad \) とおくと、④ から
      \(\displaystyle \qquad \dfrac{x^2}{a^2}\ +\ \dfrac{y^2}{b^2}\ =\ 1\quad (a\ \gt\ b\ \gt\ 0),\quad F (-ae,\ 0),\quad l:\ x\ =\ -\dfrac{a}{e} \)
      このとき、⑤、⑥ から \( c \) を消去すると \(\displaystyle \quad e\ =\ \dfrac{ \sqrt{a^2\ -\ b^2} }{a} \)

   2. \(\quad 1\ \lt\ e\ \) のとき

      \(\displaystyle a\ =\ \dfrac{ce}{e^2\ -\ 1} \cdots\ ⑦, \quad b\ =\ \dfrac{ce}{\sqrt{e^2\ -\ 1}}\ \cdots\ ⑧\quad \) とおくと、④ から
      \(\displaystyle \qquad \dfrac{x^2}{a^2}\ -\ \dfrac{y^2}{b^2}\ =\ 1\quad (a\ \gt\ 0,\ b\ \gt\ 0),\quad F (ae,\ 0),\quad l:\ x\ =\ \dfrac{a}{e} \)
      このとき、⑦、⑧ から \( c \) を消去すると \(\displaystyle \quad e\ =\ \dfrac{ \sqrt{a^2\ +\ b^2} }{a} \)