極座標と直交座標
 極座標と極方程式
極座標と極方程式極座標
極 \( O \)、始線 \( OX \) に対し、\( OP\ =\ r \)、\( OX \) から半直線 \( OP \) へ測った角を \( \theta \) とすると、点 \( P \) の 極座標 は \(\ (r,\ 0)\ \) で表される。
極 \( O \) の極座標は、\( \theta \) を任意の実数として \(\ (0,\ \theta)\ \) と定める。また、極 \( O \) 以外の点に対して、例えば \(\ 0\ \leqq\ \theta\ \lt 2 \pi\ \) と制限すると、点 \( P \) の極座標は1通りに定まる。
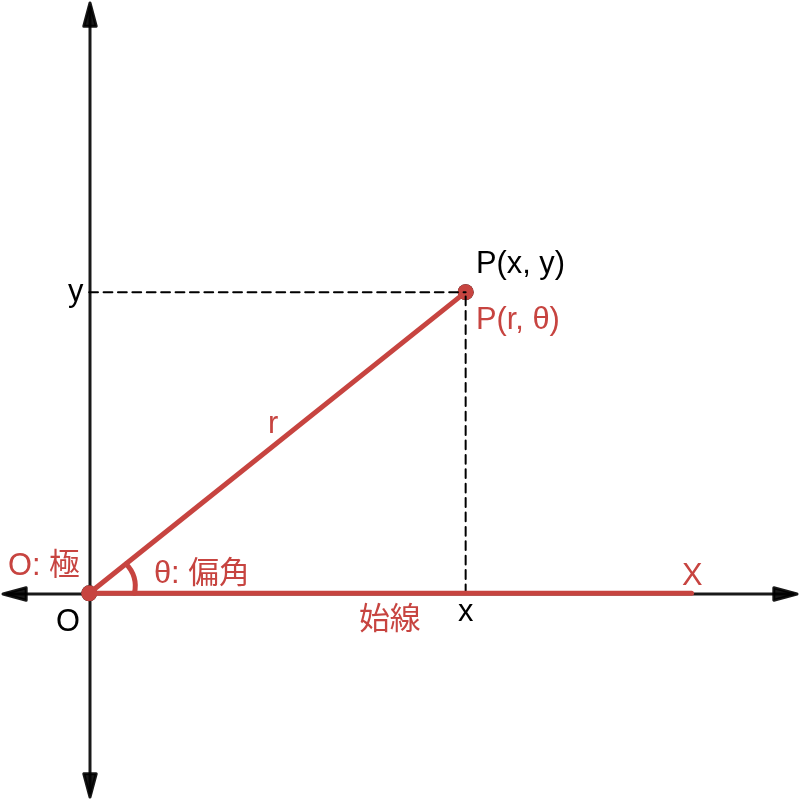
平面上に点 \( O \) と半直線 \( XO \) を定めると、平面上の任意の点 \( P \) の位置は、\( OP \) の長さ \( r \) と、\( OX \) から半直線 \( OP \) へ測った角 \( \theta \) で決まる (ただし、\( \theta \) は弧度法で表した一般角である)。
このとき、\(\ (r,\ \theta)\ \) を点 \( P \) の 極座標 といい、角 \( \theta \) を 偏角、定点 \( O \) を 極、半直線 \( XO \) を 始線 という。
極座標では \(\ (r,\ \theta)\ \) と \(\ (r,\ \theta\ +\ 2n\pi)\ \) [\( n \) は整数]は同じ点を表すが、極座標による点の表し方を1通りにするため、偏角 \( \theta \) を例えば \(\ 0\ \leqq\ 0\ \lt 2 \pi\ \) とすることがある。
極座標に対し、これまで用いてきた \( x \) 座標、 \( y \) 座標の組 \(\ (x,\ y)\ \) で表した座標を 直交座標 という。座標平面において極座標を考える場合、普通、原点 \( O \) を極、\( x \) 軸の正の部分を始線とする。
極座標と直交座標
点 \( P \) の直交座標を \(\ (x,\ y)\ \)、極座標を \(\ (r,\ \theta)\ \) とすると
- \( x\ = r \cos{\theta},\quad y\ =\ r \sin{\theta} \)
- \( r\ =\ \sqrt{x^2\ +\ y^2} \)
\(\displaystyle \cos{\theta}\ =\ \dfrac{x}{r},\quad \sin{\theta}\ =\ \dfrac{y}{r}\qquad (r\ \neq 0)\)
2点間の距離、三角形の面積
\( O \) を極とする極座標に関して2点 \(\ A(r_1,\ \theta_1) \)、\(\ B(r_2,\ \theta_2) \) があるとき
- 2点 \(\ A,\ B\ \) 間の距離
- \( AB\ =\ \sqrt{ {r_1}^2\ +\ {r_2}^2\ -\ 2 r_1 r_2 \cos{(\theta_2\ -\ \theta_1)} } \)
- \( \triangle{OAB}\) の面積 \( S \)
- \(\displaystyle S\ =\ \dfrac{1}{2} r_1 r_2 |\sin{(\theta_2\ -\ \theta_1)}| \)
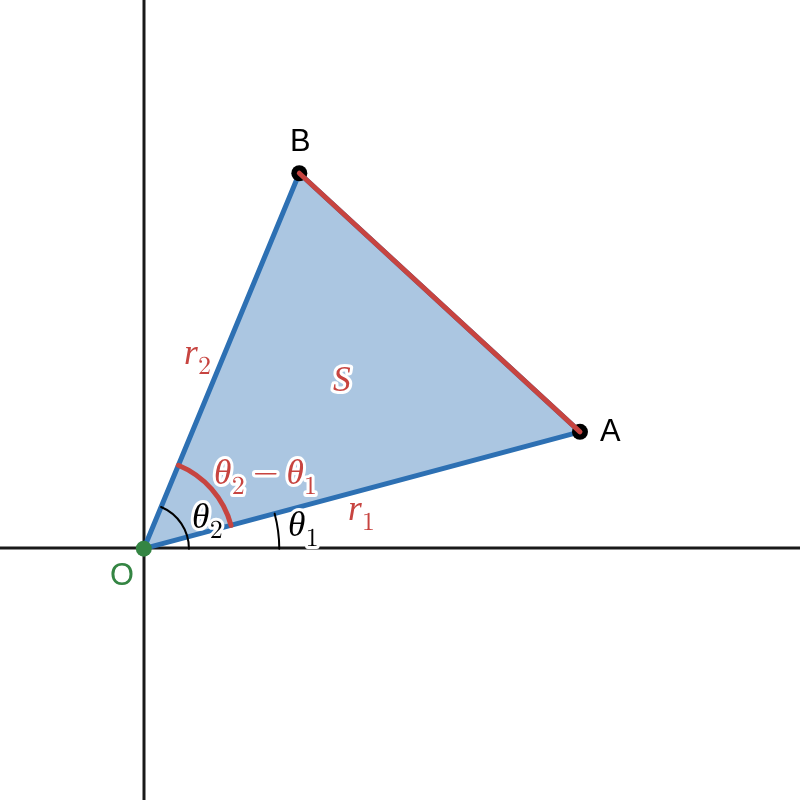
\( \triangle{OAB} \) において \( \angle{AOB}\ =\ \theta_2\ -\ \theta_1,\ OA\ =\ r_1,\ OB\ =\ r_2 \) である。
余弦定理により、\(\displaystyle \qquad AB = \sqrt{ {r_1}^2\ +\ {r_2}^2\ -\ 2 r_1 r_2 \cos{(\theta_2\ -\ \theta_1)} } \)
三角形の面積は \(\displaystyle \qquad S\ =\ \dfrac{1}{2} r_1 r_2 |\sin{(\theta_2\ -\ \theta_1)}| \)
\(\displaystyle \qquad ※ \cos{(\theta_2\ -\ \theta_1)}\ =\ \cos{(\theta_1\ -\ \theta_2)} \quad \) であるのに対し、\(\displaystyle \quad \sin{(\theta_2\ -\ \theta_1)}\ =\ -\sin{(\theta_1\ -\ \theta_2)} \quad \) なので \( \quad \sin{(\theta_2\ -\ \theta_1)} \quad \) は絶対値でなければならない