180° ‐ θ、90° ± θ の三角比

\( 90^{\circ} – \theta \)

\( \begin{eqnarray}
\sin (90^{\circ} – \theta) &=& \cos \theta \\
\cos (90^{\circ} – \theta) &=& \sin \theta \\
\tan (90^{\circ} – \theta) &=& \displaystyle \frac{1}{\tan \theta} \\
\end{eqnarray} \)
\(
(0^{\circ} \lt \theta \lt 90^{\circ})
\)

---

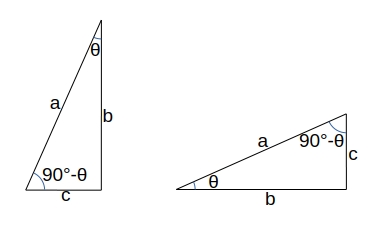
\( \begin{eqnarray}
\sin (90^{\circ} – \theta) &=& \displaystyle \frac{b}{a} \qquad \cos \theta &=& \displaystyle \frac{b}{a} \\
\cos (90^{\circ} – \theta) &=& \displaystyle \frac{c}{a} \qquad \sin \theta &=& \displaystyle \frac{c}{a} \\
\tan (90^{\circ} – \theta) &=& \displaystyle \frac{b}{c} \qquad \displaystyle \frac{1}{\tan \theta} &=& \displaystyle \frac{1}{ \frac{c}{b} } &=& \displaystyle \frac{b}{c} \\
\end{eqnarray} \)

\( 180^{\circ} – \theta \)

\( \begin{eqnarray}
\sin (180^{\circ} – \theta) &=& \sin \theta \\
\cos (180^{\circ} – \theta) &=& – \cos \theta \\
\tan (180^{\circ} – \theta) &=& – \tan \theta \\
\end{eqnarray} \)
\(
(0^{\circ} \leqq \theta \leqq 180^{\circ})
\)

---

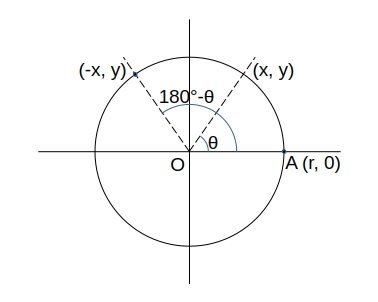
\( \begin{array}{l l}
\sin (180^{\circ} – \theta) = \displaystyle \frac{y}{r} & \sin \theta = \displaystyle \frac{y}{r} \\
\cos (180^{\circ} – \theta) = \displaystyle \frac{-x}{r} & – \cos \theta = – \displaystyle \frac{x}{r}\\
\tan (180^{\circ} – \theta) = \displaystyle \frac{y}{-x} & – \tan \theta = – \displaystyle \frac{y}{x} \\
\end{array} \)

\( 90^{\circ} + \theta \)

\( \begin{eqnarray}
\sin (90^{\circ} + \theta) &=& \cos \theta \\
\cos (90^{\circ} + \theta) &=& – \sin \theta \\
\tan (90^{\circ} + \theta) &=& – \displaystyle \frac{1}{\tan \theta} \\
\end{eqnarray} \)
\(
(0^{\circ} \leqq \theta \leqq 90^{\circ})
\)

---

\( \begin{eqnarray}
\sin (90^{\circ} + \theta) &=& \sin \{ 180^{\circ} – (90^{\circ} – \theta) \} \\
&=& \sin (90^{\circ} – \theta) \\
&=& \cos \theta \\
\end{eqnarray} \)

\( \begin{eqnarray}
\cos (90^{\circ} + \theta) &=& \cos \{ 180^{\circ} – (90^{\circ} – \theta) \} \\
&=& – \cos (90^{\circ} – \theta) \\
&=& – \sin \theta \\
\end{eqnarray} \)

\( \begin{eqnarray}
\tan (90^{\circ} + \theta) &=& \tan \{ 180^{\circ} – (90^{\circ} – \theta) \} \\
&=& – \tan (90^{\circ} – \theta) \\
&=& – \displaystyle \frac{1}{\tan \theta} \\
\end{eqnarray} \)