余弦定理
 図形と計算
図形と計算\( \triangle ABC \) において
\( \begin{eqnarray}
a^2 &=& b^2 + c^2\ -\ 2bc \cdot cos A \qquad \cos A &=& \displaystyle \frac{b^2 + c^2\ -\ a^2}{2bc} \\
b^2 &=& c^2 + a^2\ -\ 2ca \cdot cos B \qquad \cos B &=& \displaystyle \frac{c^2 + a^2\ -\ b^2}{2ca} \\
c^2 &=& a^2 + b^2\ -\ 2ab \cdot cos C \qquad \cos C &=& \displaystyle \frac{a^2 + b^2\ -\ c^2}{2ab} \\
\end{eqnarray} \)
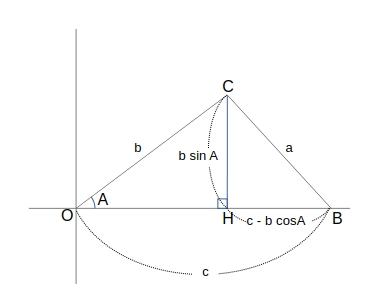
座標軸上に 頂点 \( A \) が原点、辺 \( AB \) が \( x \) 軸 の正の部分になるように \( \triangle ABC \) を描くと、
頂点 \( A \)、頂点 \( B \)、頂点 \( C \) の座標はそれぞれ \( A (0, 0) \)、\( B (c, 0) \)、\( C (b \cos A, b sin A) \) になる。
頂点 \( C \) から 辺 \( AB \) に垂線を引き 辺 \( AB \) との交点を \( H \) とすると、\( \triangle BCH \) は直角三角形なので
\( \begin{eqnarray}
BC^2 &=& BH^2 + CH^2 \\
a^2 &=& (c – b \cos A)^2 + (b \sin A)^2 \\
&=& c^2 – 2 b c \cos A + b^2 \cos^2 A + b^2 \sin^2 A \\
&=& c^2 – 2 b c \cos A + b^2 (\cos^2 A + \sin^2 A) \\
&=& b^2 + c^2 – 2 b c \cos A \\
\end{eqnarray} \)