内心

三角形の３つの内角の二等分線は１点で交わり、その点は３つの辺から当距離にある。

---

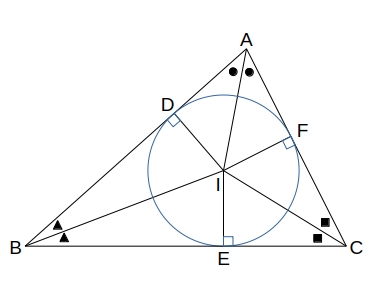
\( \triangle ABC \) で \( \angle B \) と \( \angle C \) の二等分線の交点を \( I \) とし、\( I \) から \( 辺AB \)、\( 辺BC \)、 \( 辺CA \) に下ろした垂線と各辺の交点を \( D \)、\( E \)、\( F \) とする。

\( \triangle BID \) と \( \triangle BIE \) は \( \angle BDI = \angle BEI = \angle R \) であり、\( 斜辺BI \) を共有し、\( \angle DBI = \angle EBI \) なので合同であり、\( ID = IE \) である。
同様に、\( \triangle CIE \) と \( \triangle CIF \) は合同であり、\( IE = IF \) である。

\( \triangle AID \) と \( \triangle AIF \) は \( \angle ADI = \angle AFI = \angle R \) であり、\( 斜辺AI \) を共有し、他の一辺 \( ID = IF \) なので合同である。
したがって \( \angle DAI = \angle FAI \) であり、つまり、\( 点I \) は \( \angle A \) の二等分線上にもある。

よって、三角形の３つの内角の２等分線は１点で交わり、その点は３辺から等距離にある。