重心

三角形の３つの中線は一点で交わり、その点は各中線を \( 2:1 \) に内分する。

---

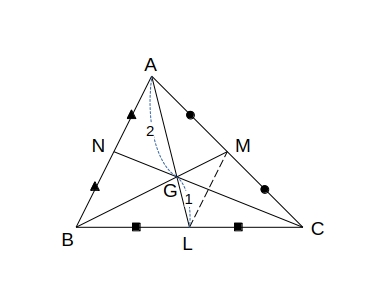
\( \triangle ABC \) の \( 辺AB \)、 \( BC \)、 \( CA \) の中点をそれぞれ \( L \)、\( M \)、\( N \) とする。

\( 点L \)、\( 点M \) はそれぞれ \( 辺BC \)、 \( CA \) の中点であるから、\( ML // AB \) かつ \( 2ML = AB \) である。
\( 中線AL \) と \( 中線BM \) の交点を \( G \) とすると、\( AG:GL = BG:GM = 2:1 \) となる。

同様に、\( 中線BM \) と \( 中線CN \) の交点を \( G’ \) とすると、\( BG’:G’M = CG’:G’N = 2:1 \) となる。

\( G \) と \( G’ \) はともに \( 線分BM \) を \( 2:1 \) に内分する点であるから、この２点は一致する。

したがって、三角形の３つの中線は一点で交わり、その点は各中線を \( 2:1 \) に内分する。