方べきの定理I

\

円の2つの \(弦 AB, CD \) の交点、またはそれらの延長の交点を \( P \) とすると、\( PA \cdot PB = PC \cdot PD \) が成り立つ

---

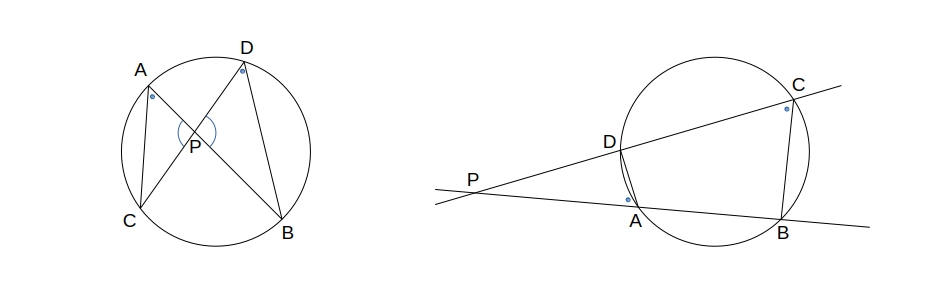
\( \triangle PAC \) と \( \triangle PDB \) において、
\( \begin{eqnarray}
\angle CAP &=& \angle BDP \\
\angle APC &=& \angle DPB \\
\end{eqnarray} \)
なので
\(
\triangle PAC \sim \triangle PDB
\)
である。

したがって、
\( \begin{eqnarray}
PA:PD &=& PC:PB \\
\therefore PA \cdot PB &=& PC \cdot PD
\end{eqnarray} \)