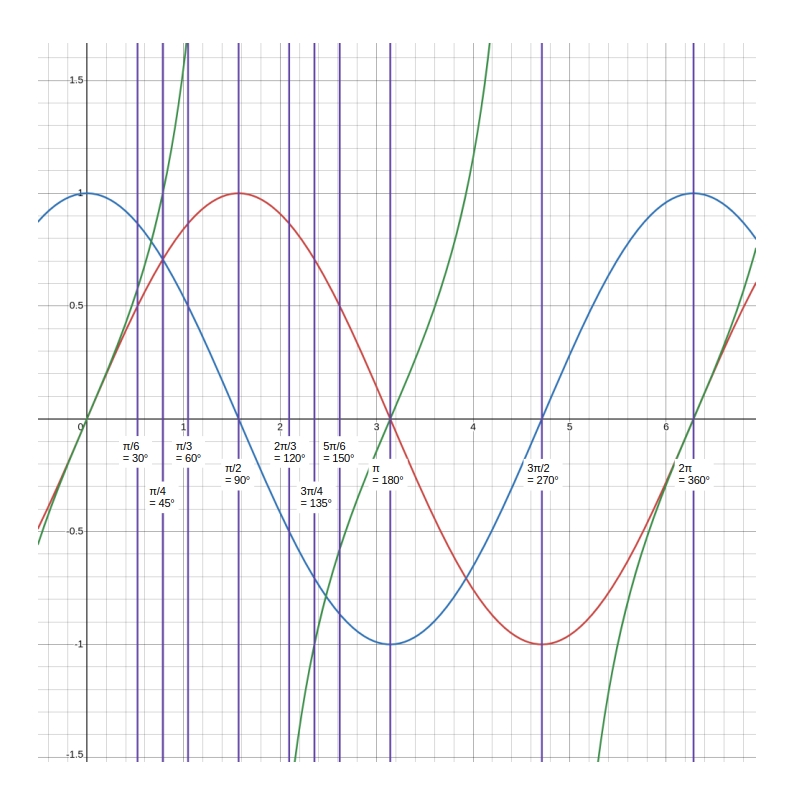
三角関数の性質
 三角関数
三角関数\( \theta + 2n \pi \) の三角関数 ( \(n\) は整数)
\( \sin (\theta + 2n \pi) = \sin \theta \)
\( \cos (\theta + 2n \pi) = \cos \theta \)
\( \tan (\theta + 2n \pi) = \tan \theta \)
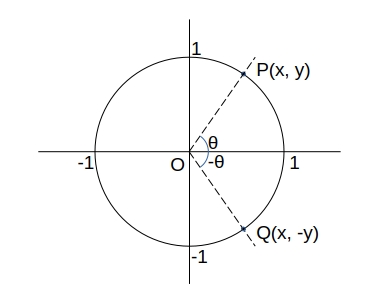
\( – \theta \) の三角関数
\( \sin(- \theta) = -y = – \sin \theta \)
\( \cos(- \theta) = x = \cos \theta \)
\( \tan(- \theta) = \dfrac{-y}{x}= – \tan \theta \)
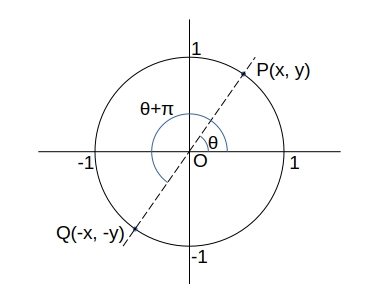
\( \theta + \pi \) の三角関数
\( \sin(\theta + \pi) = -y = – \sin \theta \)
\( \cos(\theta + \pi) = -x = – \cos \theta \)
\( \tan(\theta + \pi) = \dfrac{-y}{-x}= \tan \theta \)
この式の \( \theta \) を \( – \theta \) とすると、
\( \sin( \pi – \theta ) = – \sin ( – \theta ) = \sin \theta \)
\( \cos( \pi – \theta ) = – \cos ( – \theta ) = – \cos \theta \)
\( \tan( \pi – \theta ) = \tan ( – \theta ) = – \tan \theta \)
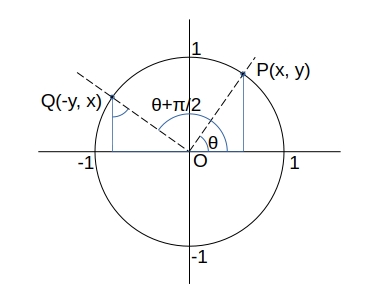
\( \theta + \dfrac{\pi}{2} \) の三角関数
\( \sin \left( \theta + \dfrac{\pi}{2} \right) = x = \cos \theta \)
\( \cos \left( \theta + \dfrac{\pi}{2} \right) = -y = – \sin \theta \)
\( \tan \left( \theta + \dfrac{\pi}{2} \right) = \dfrac{x}{-y}= – \dfrac{1}{\tan \theta} \)
この式の \( \theta \) を \( – \theta \) とすると、
\( \sin \left( \dfrac{\pi}{2} – \theta \right) = \cos ( – \theta ) = \cos \theta \)
\( \cos \left( \dfrac{\pi}{2} – \theta \right) = – \sin (- \theta ) = \sin \theta \)
\( \tan \left( \dfrac{\pi}{2} – \theta \right) = – \dfrac{1}{\tan (- \theta )} = \dfrac{1}{\tan \theta} \)