放物線

放物線 \(\qquad y^2 = 4px\quad (p \neq 0)\qquad \) [標準形]

1. 頂点は原点、
   焦点は 点 \( (p,\ 0) \)
   準線は 直線 \( x = -p \)
2. 軸は \( x \)軸で、放物線は軸に関して対称。
3. 放物線上の任意の点から焦点、準戦までの距離は等しい。

---

放物線

定点 \(F\) と \(F\) を通らない定直線 \(l\) からの距離が等しい点の軌跡を 放物線 といい、点 \(F\) をその 焦点 、直線 \(l\) をその 準線 という。また、焦点を通り準線に垂直な直線を放物線の 軸 といい、軸と放物線の交点を放物線の 頂点 という。
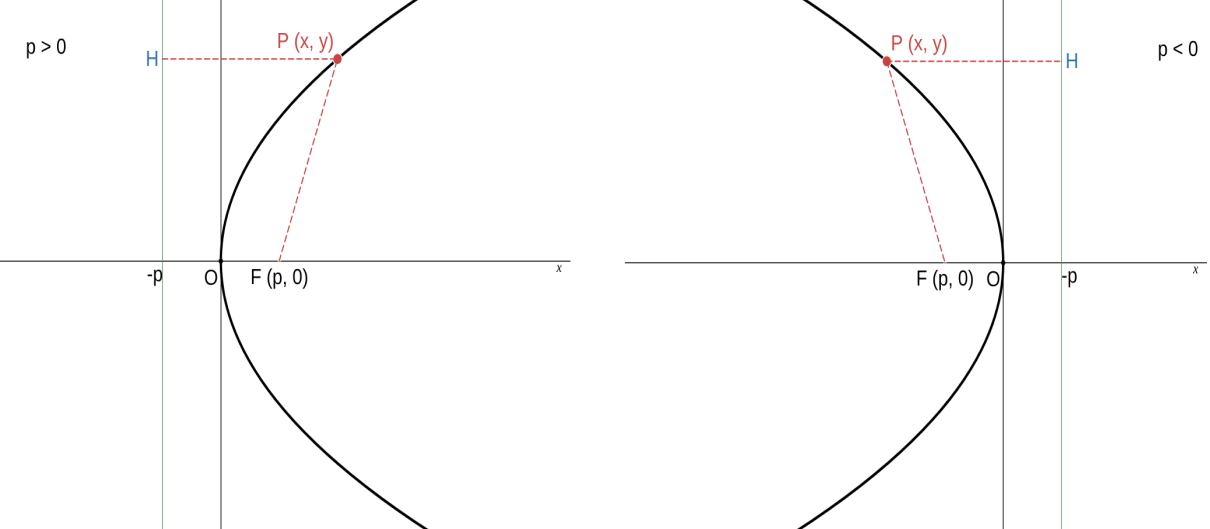
点 \(F\ (p,\ 0)\ [p \neq 0]\) を焦点とし、直線 \( l:\ x = -p \) を準線とする放物線を \( C \) とする。
\( C \) 上の点を \(P (x,\ y) \)、点 \( P \) から \( l \) におろした垂線を \( PH \) とすると、
\(\qquad PF = PH \qquad \) から \(\qquad \sqrt{ (x\ -\ p)^2 + y^2} = |x\ -\ (-p)| \)
両辺を平方して整理すると \(\quad y^2 = 4px \cdots ①\quad \) が導かれる。
逆に、\( ① \) を満たす点 \(P\ (x,\ y) \) は \( PF = PH \) を満たす。
\( ① \) を放物線の方程式の 標準形 といい、放物線 \( ① \) の軸は \(x\) 軸である。