加法定理

\( \sin (\alpha \pm \beta) = \sin \alpha \cdot \cos \beta \pm \cos \alpha \cdot \sin \beta \quad (複号同順) \)
\( \cos (\alpha \pm \beta) = \cos \alpha \cdot \cos \beta \mp \sin \alpha \cdot \sin \beta \quad (複号同順) \)
\( \tan (\alpha \pm \beta) = \dfrac {\tan \alpha \pm \tan \beta} {1 \mp \tan \alpha \cdot \tan \beta} \quad (複号同順) \)

\( \cos (\alpha – \beta) = \cos \alpha \cdot \cos \beta + \sin \alpha \cdot \sin \beta \, の証明 \)

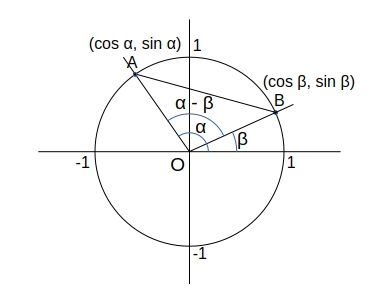
上図で \( AB^2 \) を距離の公式で表すと、
\( \begin{eqnarray*}
AB^2 &=& (\cos \alpha \,-\, \cos \beta)^2 + (\sin \alpha \,-\, \sin \beta)^2 \\
&=& ( \cos^2 \alpha \,-\, 2 \cdot \cos \alpha \cdot \cos \beta + \cos^2 \beta ) + ( \sin^2 \alpha \,-\, 2 \cdot \sin \alpha \cdot \sin \beta + \sin^2 \beta ) \\
&=& \sin^2 \alpha + \cos^2 \alpha + \sin^2 \beta + \cos^2 \beta \,-\, 2 \cdot \cos \alpha \cdot \cos \beta \,-\, 2 \cdot \sin \alpha \cdot \sin \beta \\
&=& 2 \,-\, 2 (\cos \alpha \cdot \cos \beta + \sin \alpha \cdot \sin \beta) \\
\end{eqnarray*} \)

一方、\( AB^2 \) を余弦定理で表すと、
\( \begin{eqnarray*}
AB^2 &=& 1^2 + 1^2 \,-\, 2 \cdot 1 \cdot 1 \cdot \cos( \alpha -\beta) \\
&=& 2 \,-\, 2 \cdot \cos( \alpha -\beta) \\
\end{eqnarray*} \)

従って、
\( \cos( \alpha -\beta) = \cos \alpha \cdot \cos \beta + \sin \alpha \cdot \sin \beta \)

その他の式の証明

\( \cos( \alpha -\beta) = \cos \alpha \cdot \cos \beta + \sin \alpha \cdot \sin \beta \ldots ① \) とする。

\( \cos (\alpha + \beta) = \cos \alpha \cdot \cos \beta \,-\, \sin \alpha \cdot \sin \beta \, の証明 \)

等式 ① の \( \beta \) を \( -\beta \) で置き換えると、
\( \begin{eqnarray*}
\cos \{\alpha \,-\, (-\beta)\} &=& \cos \alpha \cdot \cos (-\beta) \,+\, \sin \alpha \cdot \sin (-\beta) \\
\cos (\alpha \,+\, \beta) &=& \cos \alpha \cdot \cos \beta \,+\, \sin \alpha \cdot (-\sin \beta) \\
\cos (\alpha \,+\, \beta) &=& \cos \alpha \cdot \cos \beta \,-\, \sin \alpha \cdot \sin \beta \\
\end{eqnarray*} \)

\( \sin (\alpha + \beta) = \sin \alpha \cdot \cos \beta + \cos \alpha \cdot \sin \beta \, の証明 \)

等式 ① の \( \alpha \) を \( \left( \dfrac{\pi}{2} \,-\, \alpha \right) \) で置き換えると、
\( \begin{eqnarray*}
\cos \left\{ \left( \dfrac{\pi}{2} \,-\, \alpha \right) \,-\, \beta \right\} &=& \cos \left( \dfrac{\pi}{2} \,-\, \alpha \right) \cdot \cos \beta \,+\, \sin \left( \dfrac{\pi}{2} \,-\, \alpha \right) \cdot \sin \beta \\
\cos \left\{ \dfrac{\pi}{2} \,-\, \left( \alpha \,+\, \beta \right) \right\} &=& \cos \left( \dfrac{\pi}{2} \,-\, \alpha \right) \cdot \cos \beta \,+\, \sin \left( \dfrac{\pi}{2} \,-\, \alpha \right) \cdot \sin \beta \\
\sin \left( \alpha \,+\, \beta \right) &=& \sin \alpha \cdot \cos \beta \,+\, \cos \alpha \cdot \sin \beta \\
\end{eqnarray*} \)

\( \sin (\alpha \,-\, \beta) = \sin \alpha \cdot \cos \beta \,-\, \cos \alpha \cdot \sin \beta \, の証明 \)

\( \sin ( \alpha \,+\, \beta ) = \sin \alpha \cdot \cos \beta \,+\, \cos \alpha \cdot \sin \beta \ldots ② \) とする。

等式 ② の \( \beta \) を \( – \beta \) で置き換えると、
\( \begin{eqnarray*}
\sin \{ \alpha \,+\, (- \beta ) \} = \sin \alpha \cdot \cos ( – \beta ) \,+\, \cos \alpha \cdot \sin ( – \beta) \\
\sin ( \alpha \,-\, \beta ) = \sin \alpha \cdot \cos \beta \,+\, \cos \alpha \cdot ( – \sin \beta ) \\
\sin ( \alpha \,-\, \beta ) = \sin \alpha \cdot \cos \beta \,-\, \cos \alpha \cdot \sin \beta \\
\end{eqnarray*} \)

\( \tan (\alpha + \beta) = \dfrac {\tan \alpha + \tan \beta} {1 \,-\, \tan \alpha \cdot \tan \beta} \) の証明

\( \begin{eqnarray*}
\tan (\alpha + \beta) &=& \dfrac{\sin (\alpha + \beta) }{\cos (\alpha + \beta) } \\
&=& \dfrac {\sin \alpha \cdot \cos \beta + \cos \alpha \cdot \sin \beta} {\cos \alpha \cdot \cos \beta – \sin \alpha \cdot \sin \beta} \\[10pt]
&=& \dfrac {\dfrac {\sin \alpha \cdot \cos \beta + \cos \alpha \cdot \sin \beta} {\cos \alpha \cdot \cos \beta}} {\dfrac {\cos \alpha \cdot \cos \beta – \sin \alpha \cdot \sin \beta} {\cos \alpha \cdot \cos \beta}} \\[10pt]
&=& \dfrac {\dfrac {\sin \alpha } {\cos \alpha} + \dfrac {\sin \beta} {\cos \beta}} {\dfrac {\cos \alpha \cdot \cos \beta} {\cos \alpha \cdot \cos \beta} – \dfrac {\sin \alpha \cdot \sin \beta} {\cos \alpha \cdot \cos \beta}} \\[10pt]
&=& \dfrac {\tan \alpha + \tan \beta} {1 \,-\, \tan \alpha \cdot \tan \beta}
\end{eqnarray*} \)

\( \tan (\alpha \,-\, \beta) = \dfrac {\tan \alpha \,-\, \tan \beta} {1 \,+\, \tan \alpha \cdot \tan \beta} \) の証明

\( \tan (\alpha + \beta) = \dfrac {\tan \alpha + \tan \beta} {1 \,-\, \tan \alpha \cdot \tan \beta} \ldots ③ \) とする。

等式 ③ の \( \beta \) を \( – \beta \) で置き換えると、
\( \begin{eqnarray*}
\tan \{ \alpha + (- \beta) \} &=& \dfrac {\tan \alpha + \tan (- \beta)} {1 \,-\, \tan \alpha \cdot \tan (- \beta) } \\[10pt]
\tan \{ \alpha \,-\, \beta) \} &=& \dfrac {\tan \alpha + (- \tan \beta)} {1 \,-\, \tan \alpha \cdot (- \tan \beta) } \\[10pt]
\tan \{ \alpha \,-\, \beta) \} &=& \dfrac {\tan \alpha \,-\, \tan \beta} {1 \,+\, \tan \alpha \cdot \tan \beta} \\[10pt]
\end{eqnarray*} \)