弧度法
 三角関数
三角関数弧度法
半径 \( r \) の円で、半径に等しい長さの 弧 \( AB \) に対する中心角の大きさを 1 ラジアンという。
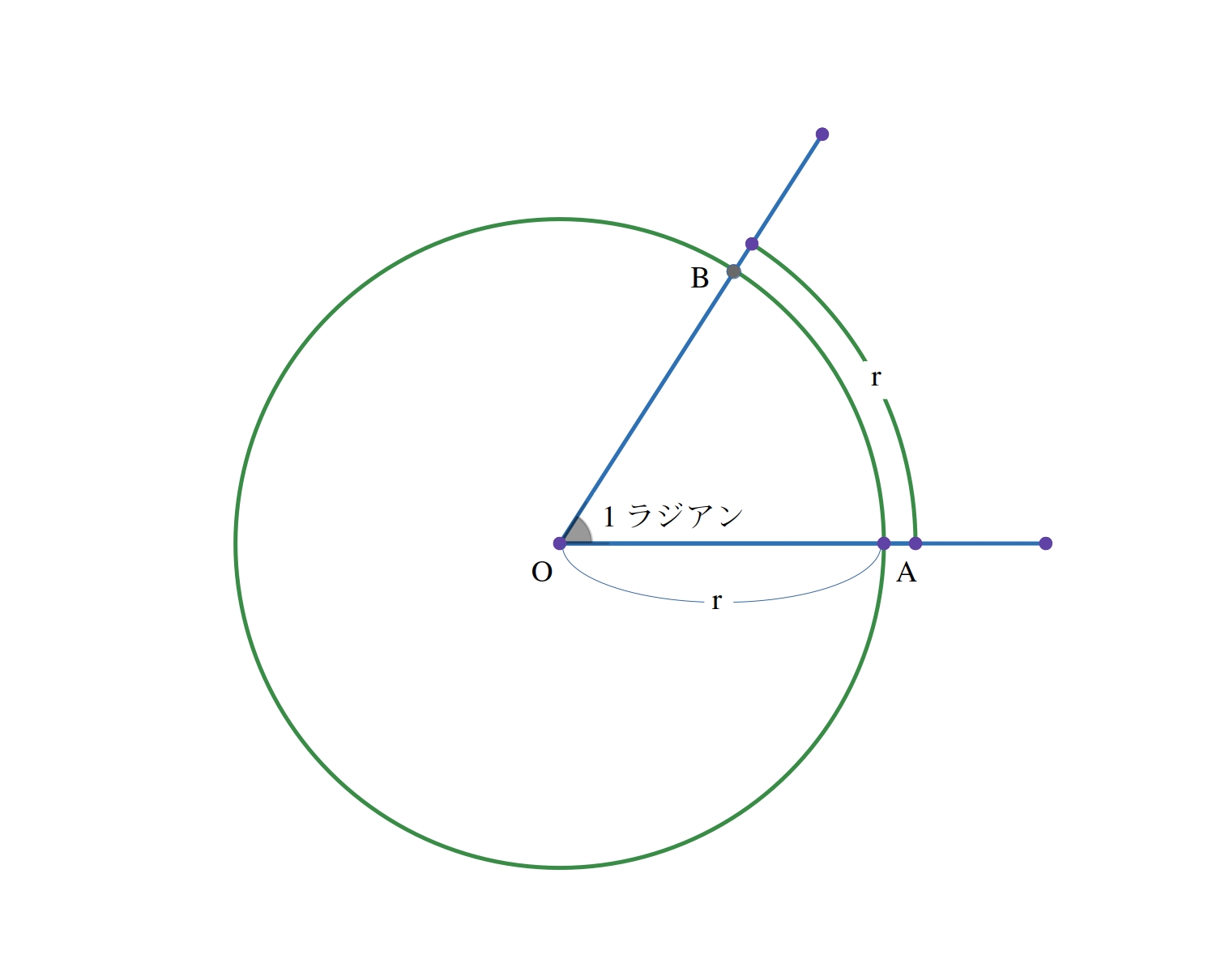
半径 \( r \) の円で長さが \( r \) である弧に対する中心角の大きさを \( a^\circ \) とすると、弧の長さと中心角の大きさは比例するから \( \dfrac {r}{2 \pi r} = \dfrac {a^\circ}{360^\circ} \)
よって、\( a^\circ = \dfrac {360^\circ} {2 \pi} \fallingdotseq 57.3^\circ \)
つまり、\( 1 ラジアン = \left( \dfrac {180} {\pi} \right) ^\circ \)、\( 180^\circ = \pi ラジアン \) である。
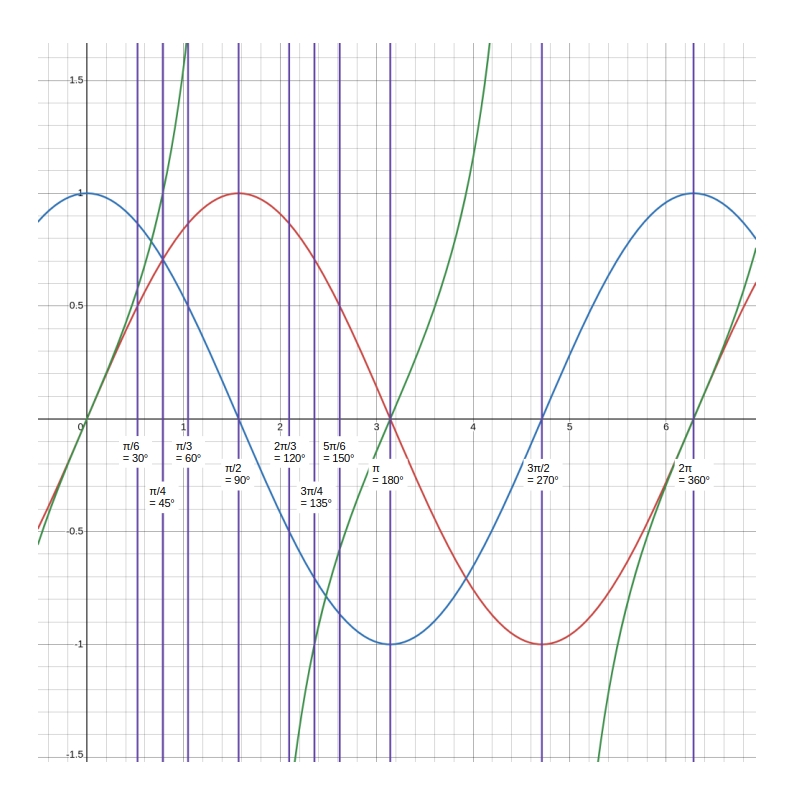
| 度数法 | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 270° | 360° |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 弧度法 | 0 | \(\dfrac{\pi}{6}\) | \(\dfrac{\pi}{4}\) | \(\dfrac{\pi}{3}\) | \(\dfrac{\pi}{2}\) | \(\dfrac{2}{3}\pi\) | \(\dfrac{3}{4}\pi\) | \(\dfrac{5}{6}\pi\) | \( \pi \) | \(\dfrac{3}{2}\pi\) | \( 2\pi \) |
| sin | 0 | \(\dfrac{1}{2}\) | \(\dfrac{\sqrt 2}{2}\) | \(\dfrac{\sqrt 3}{2}\) | 1 | \(\dfrac{\sqrt 3}{2}\) | \(\dfrac{\sqrt 2}{2}\) | \(\dfrac{1}{2}\) | \( 0 \) | \( -1 \) | \( 0 \) |
| cos | 1 | \(\dfrac{\sqrt 3}{2}\) | \(\dfrac{\sqrt 2}{2}\) | \(\dfrac{1}{2}\) | 0 | \(- \dfrac{1}{2}\) | \(- \dfrac{\sqrt 2}{2}\) | \(- \dfrac{\sqrt 3}{2}\) | \( -1 \) | \( 0 \) | \( 1 \) |
| tan | 0 | \(\dfrac{\sqrt 3}{3}\) | \( 1 \) | \(\sqrt 3\) | \( \infty \) | \(- \sqrt 3 \) | \( -1 \) | \(- \dfrac{\sqrt 3}{3}\) | \( 0 \) | \( \infty \) | \( 0 \) |
扇形の弧の長さ
弧の長さを \( l \) とする。
\( l = 2 \pi r \cdot \dfrac{\theta}{2 \pi} = r \theta\)
扇形の面積
扇型の面積を \( S \) とする。
\( S = \pi r^2 \cdot \dfrac{\theta}{2 \pi} = \dfrac{1}{2} r^2 \theta\)