2直線の平行、垂直
 図形と方程式
図形と方程式
\(
2直線 \quad
\left\{
\begin{array} {l}
y = m_1x + n_1 \\
y = m_2x + n_2 \\
\end{array}
\right.
\quad において、
\
\begin{array} {l l}
m_1 = m_2 のとき & 2直線は平行 \\
m_1 \cdot m_2 = -1 のとき & 2直線は直交 \\
\end{array}
\)
\(
2直線 \quad \left\{
\
\begin{array}{l}
a_1x + b_1y + c = 0 \\
a_2x + b_2y + c = 0 \\
\end{array}
\
\right. \quad において、
\
\begin{array} {l l}
a_1 b_2\ -\ a_2 b_1\ =\ 0 のとき & 2直線は平行 \\
a_1 a_2 + b_1 b_2 = 0 のとき & 2直線は直交 \\
\end{array}
\)
\(
\begin{array}{l}
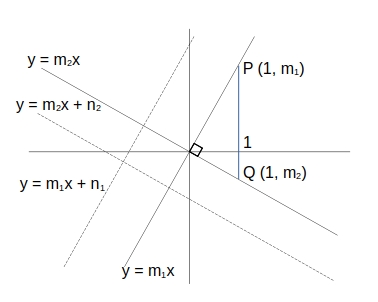
y = m_1x + n_1\ に平行で\ 原点 O\ を通る直線\ y = m_1x\ 上に\ 点 P (1, m_1)\ を、 \\
また、y = m_2x + n_2\ に平行で\ 原点 O\ を通る直線\ y = m_2x\ 上に\ 点 Q (1, m_2)\ を取る。 \\
\end{array}
\)
\(
2直線が直行する時\ OP \perp OQ\ であり、OP^2 + OQ^2 = PQ^2 である。
\)
\(
\begin{eqnarray}
\therefore \quad ({m_1}^2 + 1^2) + ({m_2}^2 + 1^2) &=& (m_1 – m_2)^2 \\
{m_1}^2 + {m_2}^2 + 2 &=& {m_1}^2 – 2 m_1 m_2 + {m_2}^2 \\
2 &=& -2 m_1 m_2 \\
よって、\quad m_1 m_2 &=& -1
\end{eqnarray}
\)
\(
2直線 \quad \left\{
\
\begin{array}{l l}
a_1x + b_1y + c = 0 & \ldots ① \\
a_2x + b_2y + c = 0 & \ldots ② \\
\end{array}
\
\right. \quad において、
\
\begin{array}{l l}
①\ の傾きは & \displaystyle -\ \frac{a_1}{b_1} \\
②\ の傾きは & \displaystyle -\ \frac{a_2}{b_2} \\
\end{array}
\
\quad である。
\)
\( \begin{array}{l}
2直線が平行である時、 \\
\displaystyle -\ \frac{a_1}{b_1} = \displaystyle -\ \frac{a_2}{b_2} \\
\therefore a_1 b_2\ -\ a_2 b_1\ =\ 0 \\
\end{array} \)
\( \begin{array}{l}
2直線が直行する時、 \\
\left( \displaystyle -\ \frac{a_1}{b_1} \right) \left( \displaystyle -\ \frac{a_2}{b_2} \right) = -1 \\
\therefore a_1 a_2 + b_1 b_2 = 0 \\
\end{array} \)