点と直線の距離

点 \( P (x_p, y_p) \) と 直線 \( l = ax + by + c = 0 \) との距離 \( h \) は
\(
h = \displaystyle \frac{ |ax_p + by_p + c| }{ \sqrt{a^2 + b^2} }
\)

---

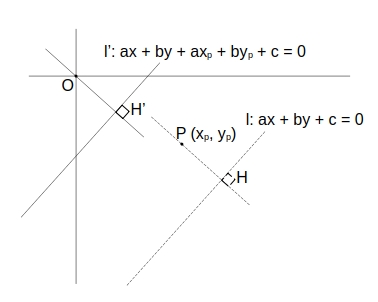
\( 点P \) が原点となるように全体を平行移動すると \( 直線 l \) の移動後の \( 直線 l’ \) は
\( \begin{eqnarray}
l’: a(x + x_p) + b(y + y_p) + c &=& 0 \\
ax + by + ax_p + by_p + c &=& 0 \\
\end{eqnarray} \)
であり、\( ax_p + by_p + c = d \) とすると
\( l’: ax + by + d = 0 \quad \ldots ① \)

一方で、原点を通り \( l’ \) と直交する直線は
\( l’: bx – ay = 0 \quad \ldots ② \)
である。

\( \begin{array}{l l}
① \times a + ② \times b より、& (a^2 + b^2)x + ad = 0 \\
① \times b – ② \times a より、& (a^2 + b^2)y + bd = 0 \\
\end{array} \)

よって、① と ② の交点 \( H’ \) の座標は、
\(
H’: \left( – \displaystyle \frac{ad}{a^2 + b^2} , – \displaystyle \frac{bd}{a^2 + b^2} \right)
\)

であり、\( 点O \) と \( 点H’ \) の距離 \( h \) は
\(
\begin{eqnarray}
h &=& \sqrt{ { \left( – \displaystyle \frac{ad}{a^2 + b^2} \right) }^2 + { \left( – \displaystyle \frac{bd}{a^2 + b^2} \right) }^2 } \\
&=& \sqrt{ \displaystyle \frac{ (a^2 + b^2)d^2 }{ (a^2 + b^2)^2 } } \\
&=& \frac{ |d| }{ \sqrt{(a^2 + b^2)} } \\
&=& \frac{ |ax_p + by_p + c| }{ \sqrt{a^2 + b^2} } \\
\end{eqnarray}
\)